
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Теорема множення ймовірностей
Теорема множення ймовірностей формулюється в такий спосіб.
Імовірність добутку двох подій дорівнює добутку ймовірності однієї з них на умовну ймовірність іншої, обчислену за умови, що перша мала місце
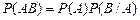 . (12)
. (12)
Доведемо теорему множення для схеми випадків.
Нехай можливі наслідки досліду зводяться до 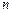 випадків. Припустимо, що події
випадків. Припустимо, що події 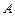 сприяє
сприяє 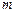 випадків, а події
випадків, а події 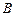 сприяє
сприяє  випадків. Події не припускаються несумісними, тому взагалі існують випадки, сприятливі й події
випадків. Події не припускаються несумісними, тому взагалі існують випадки, сприятливі й події 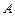 , й події
, й події 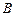 разом. Нехай число таких випадків
разом. Нехай число таких випадків  , тоді
, тоді
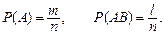
Обчислимо  умовну ймовірність події
умовну ймовірність події 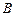 в припущенні, що подія
в припущенні, що подія 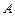 мала місце. Якщо відомо, що подія
мала місце. Якщо відомо, що подія 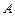 відбулася, то з раніше можливих
відбулася, то з раніше можливих 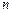 випадків залишаються можливими тільки ті
випадків залишаються можливими тільки ті 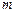 , які сприятливі події
, які сприятливі події 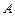 . З них
. З них  випадків сприятливі події
випадків сприятливі події 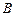 . Отже,
. Отже,
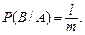
Підставляючи вирази 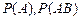 й
й 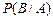 у формулу (12), одержимо тотожність. Теорему доведено.
у формулу (12), одержимо тотожність. Теорему доведено.
Очевидно, при доказі теореми множення не принципово, яке з подій 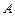 і
і 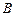 вважати першим, а яке другим, тому результат може бути записаний і в такому вигляді
вважати першим, а яке другим, тому результат може бути записаний і в такому вигляді
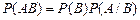 .
.
Наслідки, що випливають із теореми множення.
Наслідок 1. Якщо подія 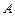 не залежить від події
не залежить від події 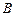 , то й подія
, то й подія 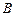 не залежить від події
не залежить від події 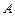 .
.
Наслідок 2. Імовірність добутку двох незалежних подій дорівнює добутку ймовірностей цих подій.
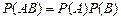 .
.
Наслідок 2 безпосередньо випливає з визначення незалежних подій, коли 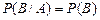 .
.
Теорема множення ймовірностей може бути узагальнена на випадок довільного числа подій. У загальному вигляді вона формулюється так.
Ймовірність добутку декількох подій дорівнює добутку ймовірностей цих подій, причому ймовірність кожної наступної події обчислюється за умови, що всі попередні мали місце. Так, для чотирьох подій.
 .
.
Приклад. Два диспетчери незалежно друг від друга передають на борт повітряного судна повідомлення в умовах завад. Імовірність прийому повідомлення від першого диспетчера становить 0,5, від другого – 0,6.
Знайти ймовірність прийому повідомлень одночасно від двох диспетчерів.
Нехай подія  прийом повідомлень від двох диспетчерів, подія
прийом повідомлень від двох диспетчерів, подія 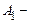 прийом повідомлення від першого диспетчера, подія
прийом повідомлення від першого диспетчера, подія  прийом повідомлення від другого диспетчера. Тоді
прийом повідомлення від другого диспетчера. Тоді  , причому
, причому  й
й  незалежні події. Тому
незалежні події. Тому
 0,3.
0,3.
Приклад. З партії, що містить  справних і
справних і 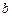 бракованих транзисторів, вилучають один за іншим два транзистори.
бракованих транзисторів, вилучають один за іншим два транзистори.
Знайти ймовірність того, що перший транзистор буде справним, а другий – бракованим.
Нехай подія  шукана подія,
шукана подія, 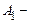 подія, що складається в тому, що перший вилучений транзистор є справним,
подія, що складається в тому, що перший вилучений транзистор є справним,  подія, що складається в тому, що другий вилучений транзистор є бракованим. Тоді
подія, що складається в тому, що другий вилучений транзистор є бракованим. Тоді  , причому в даній задачі
, причому в даній задачі  й
й  залежні події. Тому
залежні події. Тому
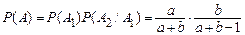 .
.
| <== попередня сторінка | | | наступна сторінка ==> |
| Теорема додавання ймовірностей | | | Формула повної ймовірності |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |