Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Закон розподілу неперервної випадкової величини

Поняття ряду розподілу, що є досить наочним і зручним, на жаль, втрачає зміст для неперервних випадкових величин. Для опису неперервної випадкової величини використовуються функція розподілу й щільність імовірності.

Для функції розподілу неперервної випадкової величини повністю зберігають свій зміст всі положення й висновки, що наведені раніше для функції розподілу дискретної випадкової величини. Це твердження випливає з наступних обставин.

Функція розподілу будь-якої дискретної випадкової величини завжди є розривна східчаста функція, стрибки якої відбуваються в точках, що відповідають можливим значенням випадкової величини, і дорівнюють ймовірностям цих значень. Сума всіх стрибків функції 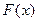дорівнює одиниці.

У міру збільшення числа можливих значень випадкової величини й зменшення інтервалів між ними, число стрибків стає більше, а величина самих стрибків – менше; східчаста крива стає усе більш плавною; дискретна випадкова величина поступово наближається до неперервної величини, а її функція розподілу – до неперервної функції (рис. 3).

Рис.3. Функція розподілу неперервної випадкової величини

Таким чином, функція розподілу неперервної випадкової величини при устремлінні до нуля інтервалів між дискретами безпосередньо слідує з функції розподілу дискретної випадкової величини й тому наслідує усі її властивості.

У задачах радіотехніки, що оперують із неперервними випадковими величинами, значно зручніше мати справу не з функцією розподілу, а з її похідною, яка називається щільністю ймовірності.

Щільністю ймовірності 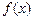випадкової величини називається похідна її функції розподілу

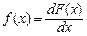. (3)

Відповідно до такого визначення щільність ймовірності часто називають диференціальним, а функцію розподілу – відповідно інтегральним законом розподілу неперервної випадкової величини.

Для пояснення сутності щільності ймовірності виділимо ще одну властивість функції розподілу.

Ймовірність попадання випадкової величини на напіввідрізок дорівнює приросту функції розподілу на цій ділянці.

. (4)

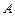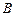Доведення. Розглянемо три події: подія , що складається в тому, що ; подія , що складається в тому, що ; подія 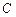, що складається в тому, що .

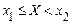З огляду на те, що , по теоремі додавання ймовірностей отримаємо

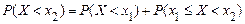що збігається з виразом (4).

Для досить малих значень 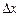з (3) слідує

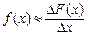Звідси щільність ймовірності 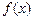є функція, що при множенні її на 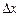дає ймовірність попадання випадкової величини в інтервал від 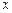до + .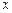

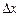Ймовірність 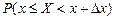пропорційна значенню щільності ймовірності в точці 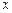. Тому 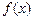можна трактувати як характеристику, що показує, наскільки ймовірно те або інше значення неперервної випадкової величини.

Щільність ймовірності є розмірною характеристикою. Її розмірність обернена розмірності неперервної випадкової величини.

Щільність ймовірності випадкової величини має наступні властивості.

1. Щільність ймовірності більше або дорівнює нулю.

2. Ймовірність попадання неперервної випадкової величини в інтервал дорівнює інтегралу від щільності ймовірності в цих межах

Отриману ймовірність можна інтерпретувати як площу, укладену між кривою 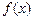й віссю абсцис у межах від 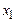до 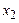(рис. 4).

Рис. 4. Щільність ймовірності неперервної випадкової величини

3. Інтеграл від щільності ймовірності, узятий у нескінченних межах, дорівнює одиниці

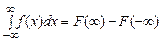=1 – 0 =1.

Приклад. Нехай всі значення 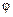випадкової початкової фази гармонійного радіосигналу, що приймають значення з відрізка 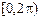, є рівноможливими.

Потрібно записати вираз для щільності ймовірності .

У силу рівної можливості спостереження всіх значень 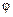із інтервалу 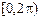,щільність повинна мати на цьому відрізку незмінне значення . Щоб знайти цю константу, скористаємося умовою нормування щільності ймовірності

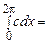1, звідки .

<== попередня сторінка	\|	наступна сторінка ==>
	\|	Числові характеристики скалярної випадкової величини

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.