Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Числові характеристики скалярної випадкової величини

У практичних задачах радіотехніки часто повний опис випадкової величини за допомогою закону розподілу можна замінити досить грубим, але більш простим зазначенням окремих параметрів (характерних чисел) цього розподілу. До них належать, насамперед, математичне сподівання й дисперсія.

Математичне сподівання випадкової величини є ймовірнісним узагальненням поняття середнього арифметичного детермінованої величини.

Нехай дослід відтворюється в незмінних умовах 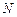раз, і при цьому досліджується випадкова величина , що 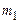раз прийняла значен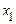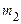ня , раз – значення , раз – значення , де .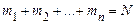

Знайдемо середнє арифметичне 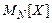значень випадкової величини в дослідах

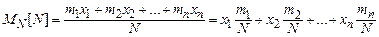У досить довгій серії дослідів відносні частоти подій, що полягають в тому, що випадкова величина приймає значення 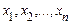, групуються біля ймовірностей 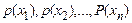цих значень. Отже, середнє арифметичне значень випадкової величини, що спостерігаються у досить довгій серії дослідів, буде групуватися навколо величини

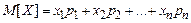яка називається середнім значенням або математичним сподіванням випадкової величини (часто для нього використовується позначення ).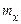

Таким чином, математичним сподіванням випадкової величини називається значення, біля якого групуються в дослідах достатньої довжини середні арифметичні її спостережуваних значень.

При цьому скільки-небудь суттєві відхилення середнього арифметичного значення випадкової величини від математичного сподівання в 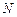дослідах будуть траплятися досить рідко. Отриманий результат далі будемо записувати у вигляді

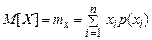. (5)

Математичне сподівання має розмірність випадкової величини.

Приклад. Випадкова величина , що характеризує струмові й безструмові посилки телеграфного сигналу, приймає два значення: одиницю з ймовірністю й нуль з ймовірністю 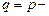1. Необхідно знайти математичне сподівання величини . З формули (5) відразу знаходимо

У ряді практичних задач виникає необхідність обчислення математичного сподівання деякої функції випадкової величини . Наприклад, енергія, яка виділяється на резисторі, пропорційна квадрату струму, що пропускається через нього.Якщо струм являє собою випадкову величину, закон розподілу якої відомий, то визначення середнього значення енергії вимагає обчислення квадратичної функції.

Очевидно, що функція випадкової величини сама являє собою випадкову величину, причому конкретне значення функції спостерігається тоді, коли випадкова величина X приймає конкретне значення з відповідною ймовірністю . Звідси слідує

. (6)

Математичне сподівання неперервної випадкової величини може бути визначене на основі можливості розгляду неперервної величини як граничного випадку дискретної.

Розіб'ємо весь інтервал значень, прийнятих неперервною випадковою величиною, на рівні відрізки досить малої довжини (рис. 5).

Рис.5. Ілюстрація щодо переходу від дискретної випадкової величини до неперервної

За значення дискретної випадкової величини приймемо значення неперервної випадкової величини на кінцях інтервалів . Ймовірність попадання випадкової величини в інтервал від до дорівнює 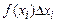. Для математичного сподівання дискретної випадкової величини одержимо . Переходячи до межі при 0, для неперервної випадкової величини знайдемо

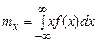. (7)

Математичне сподівання неперервної випадкової величини можна інтерпретувати як координату центра ваги фігури, укладеної між віссю абсцис і графіком щільності ймовірності (див. рис. 5).

Відповідно вираз для математичного сподівання функції неперервної випадкової величини приймає вигляд

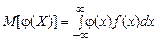. (8)

При цьому розмірність 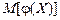збігається з розмірністю .

Властивості математичного сподівання.

1. Математичне сподівання постійної величини 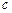дорівнює самій постійній величині

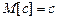Дійсно, у всіх дослідах постійна величина приймає тільки значення, рівне 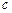. Отже, її середнє значення теж дорівнює .

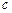2. Постійну величину можна виносити за знак математичного сподівання. Якщ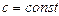о , то

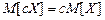3. Математичне сподівання суми (різниці) випадкових величин дорівнює сумі (різниці) їхніх математичних сподівань

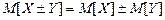Зокрема,

4. Математичне сподівання добутку незалежних випадкових величин і дорівнює добутку їхніх математичних сподівань

<== попередня сторінка	\|	наступна сторінка ==>
Закон розподілу неперервної випадкової величини	\|	ЛЕКЦІЯ 6

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.