• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ЛЕКЦІЯ 6

Введемо поняття центрованої випадкової величини. Випадкова величина називається центрованою, якщо її значення відлічуються щодо математичного сподівання.

Для центрованої випадкової величини запровадимо позначення . За визначенням

.

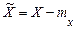Центровані випадкові величини мають дві важливі властивості.

1. Математичне сподівання центрованої випадкової величини дорівнює нулю

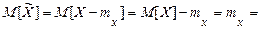0.

2. Якщо й 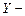незалежні випадкові величини, то 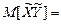0.

.

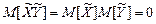Застосуємо формули для знаходження математичного сподівання функції для випадку, коли є статечною функцією

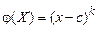, де 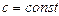, k=1,2, . . ..

Числа, які будуть отримані в результаті, називаються моментами випадкової величини відносно .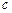

Моментом го порядку деякої випадкової величини відносно 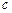називається математичне сподівання го ступеню різниці .

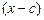Якщо 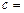0, то моменти називаються початковими, а якщо 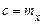, то – центральними. Початковий момент го порядку позначається через 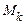, ацентральний момент го порядку .

Для дискретних і неперервних випадкових величин початкові моменти відповідно визначаються виразами

, .

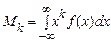Аналогічно, центральні моменти гопорядку визначаються формулами

, .

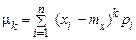Нехай 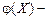функція випадкової величини . Виконаємо розкладання в статечної ряд, взявши за початкове значення випадкової величини початковий момент першого порядку (її математичне сподівання),

.

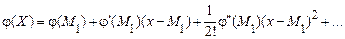Для математичного сподівання функції отримаємо

.

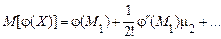Таким чином, математичне сподівання функції випадкової величини можна виразити через моменти вихідної випадкової величини, причому для цього необхідно знання незчисленної множини моментів.

Доведемо важливий факт, що складається в тому, що зі всіх моментів другого порядку випадкової величини щодо деякої постійної 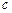, її момент щодо математичного сподівання 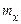є мінімальним, тобто

.

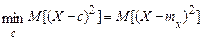Доказ. Нехай 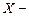неперервна випадкова величина, для якої

.

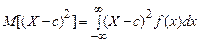З умови 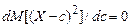знайдемо

, звідки .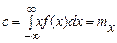

Аналогічний результатвиходить і для дискретної випадкової величини. Це означає, що постійна, яка дорівнює 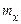, є найкращою заміною для будь-якої невідомої випадкової величини, коли за міру розходження між ними приймається середній квадрат їхньої різниці.

У радіотехніці зустрічаються задачі, для вирішення яких досить знати тільки середнє значення випадкової величини. Якщо, наприклад, відбувається відмова одного з динаміків гучномовного зв'язку в салоні повітряного судна, то звичайно це не приводить до яких-небудь важких наслідків. Тому, замінивши динамік після польоту, цікавляться тільки тим, скільки він служить у середньому. Якщо ж відбувається відмова радіостанції для зв'язку із групою керівництва польотами, то важливо, попереджаючи серйозні наслідки, замінити її трохи раніше очікуваного виходу з ладу. Тут необхідно знати не тільки середнє значення часу настання відмов, але й ступінь розкиду його можливих значень щодо цього середнього.

Як міра розсіювання випадкової величини в теорії ймовірностей використовується спеціальна характеристика, яка називається дисперсією.

Дисперсією випадкової величини називається її другий центральний момент (математичне сподівання квадрата центрованої випадкової величини).

Дисперсія випадкової величини має спеціальне позначення (іноді ).

Дисперсія дискретної випадкової величини обчислюється по формулі

, (9)

а дисперсія неперервної випадкової величини – по формулі

. (10)

З наведених виразів слідує, що чим менше дисперсія випадкової величини, тим більш компактно групуються значення цієї величини біля середнього значення .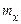

Дисперсія має розмірність квадрата випадкової величини, що не зовсім зручно, тому на практиці часто використовують ще одну характеристику розсіювання – середнє квадратичне відхилення випадкової величини, що визначається як квадратний корінь із дисперсії. Середнє квадратичне відхилення позначається через і має розмірність, що збігається з розмірністю випадкової величини.

Властивості дисперсії.

1. Дисперсія постійної величини 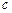дорівнює нулю.

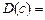0.

Ця властивість слідує з того факту, що постійна величина у всіх дослідах приймає значення 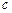, що не відрізняється від її математичного сподівання.

Вірно також зворотне твердження: якщо 0, то .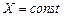

2. . Дійсно,

.

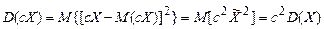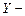3. Якщо й незалежні випадкові величини, то

.

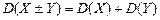4. .

Доказ.

.

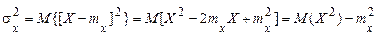Властивість (4) виражає те загальне правило, що центральні моменти випадкової величини можна за допомогою алгебраїчних співвідношень виразити через її початкові моменти.

Відзначимо, що , тобто початковий момент випадкової величини завжди не менше її центрального моменту.

Приклад. Знайдемо дисперсію випадкової величини , розглянутої в прикладі 2, яка приймає тільки два значення: одиницю з імовірністю й нуль із імовірністю 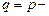1. З огляду на те, що математичне сподівання заданої випадкової величини дорівнює , з (.9) знайдемо

.

Очевидно, що дисперсія максимальна, коли 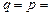1/2.

Математичне сподівання 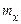й дисперсія (або середнє квадратичне відхилення ) характеризують найбільш важливі риси розподілу випадкових величин: положення й ступінь розкиду. У випадку потреби в більш докладному описі розподілу, використовуються мода, медіана й моменти вищих порядків.

Модою випадкової величини називається її найбільш імовірне значення. Для неперервної випадкової величини модою є те значення, у якому щільність імовірності максимальна.

Медіаною випадкової величини називається абсциса точки, у якій площа, що обмежена кривою розподілу цієї величини, ділиться навпіл.

У випадку, коли випадкова величина має симетричний розподіл, значення математичного сподівання, моди й медіани збігаються.

Для характеристики асиметрії розподілу випадкової величини використовується третій центральний момент.

Якщо розподіл симетричний щодо математичного сподівання, всі моменти непарного порядку дорівнюють нулю. Тому природно в якості характеристики асиметрії розподілу вибрати один з непарних моментів. Найпростішим з них є третій центральний момент. Він має розмірність куба випадкової величини, тому для одержання безрозмірної числової характеристики значення третього моменту 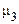ділиться на куб середнього квадратичного відхилення. Величина, що утворюється, має назву коефіцієнта асиметрії

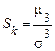. (11)

Для характеристики ексцесу (гостроти пику) розподілу випадкової величини використовується четвертий центральний момент. За значення ексцесу приймається величина

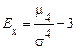. (12)

Число 3 використовується в (12) тому, що для нормального закону розподілу (який буде описаний далі) 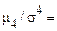3 і його ексцес дорівнює нулю.

Переглядів: 623