
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ЛЕКЦІЯ 8
Неповний, наближений опис довільного числа випадкових величин також може бути виконаний за допомогою числових характеристик. Мінімальна кількість характеристик, за допомогою якої може бути охарактеризована система 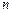 випадкових величин
випадкових величин 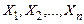 , включає:
, включає:
1. 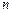 математичних сподівань
математичних сподівань  , що характеризують середні значення випадкових величин
, що характеризують середні значення випадкових величин 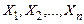 ;
;
2. 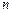 дисперсій
дисперсій 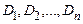 , що характеризують розсіювання випадкових величин
, що характеризують розсіювання випадкових величин 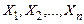 ;
;
3.  кореляційних моментів
кореляційних моментів  , що характеризують попарну кореляцію всіх величин, які входять у систему.
, що характеризують попарну кореляцію всіх величин, які входять у систему.
Сукупність всіх кореляційних моментів складає кореляційну матрицю системи. Для випадкових величин 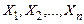 вона має вигляд
вона має вигляд
 .
.
Елементи головної діагоналі цієї матриці, що представляють собою кореляційні моменти величини 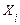 й тієї ж величини
й тієї ж величини 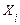 , дорівнюють дисперсіям
, дорівнюють дисперсіям 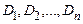 випадкових величин
випадкових величин 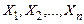
 .
.
Елементи кореляційної матриці, які розташовані симетрично стосовно головної діагоналі, попарно рівні, тому що з визначення кореляційного моменту слідує, що  .
.
Якщо випадкові величини 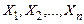 не є корельованими, то всі елементи кореляційної матриці, крім діагональних, будуть дорівнювати нулю.
не є корельованими, то всі елементи кореляційної матриці, крім діагональних, будуть дорівнювати нулю.
Таким чином, для наближеного опису системи 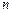 випадкових величин
випадкових величин 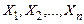 необхідно мати у своєму розпорядженні значення
необхідно мати у своєму розпорядженні значення 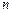 математичних сподівань
математичних сподівань  і кореляційну матрицю
і кореляційну матрицю 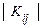 системи.
системи.
Приведемо найбільш важливі теореми про числові характеристики системи випадкових величин.
1. Математичне сподівання суми двох випадкових величин дорівнює сумі їхніх математичних сподівань
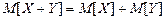 . (27)
. (27)
Доказ. Нехай 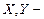 система дискретних випадкових величин. Тоді
система дискретних випадкових величин. Тоді

 .
.
Сума 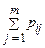 є ймовірністю того, що величина
є ймовірністю того, що величина  прийме значення
прийме значення 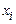 , тобто
, тобто 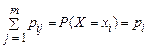 . Тому
. Тому
 .
.
Аналогічно
 .
.
Таким чином, теорему для дискретних випадкових величин доведено. Її доказ для неперервних випадкових величин цілком аналогічний.
Теорема додавання математичних сподівань узагальнюється на довільне число доданків
 .
.
2. Дисперсія суми двох випадкових величин дорівнює сумі дисперсій цих величин і їх подвоєного кореляційного моменту
 . (28)
. (28)
Доказ. Позначимо  . По теоремі додавання математичних сподівань
. По теоремі додавання математичних сподівань  . Віднімаючи з рівності
. Віднімаючи з рівності  рівність
рівність  , перейдемо від випадкових величин до відповідних центрованих випадкових величин
, перейдемо від випадкових величин до відповідних центрованих випадкових величин  . По визначенню дисперсії
. По визначенню дисперсії
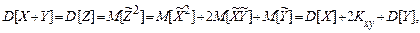
що й було потрібно довести.
Формула (28) може бути узагальнена на будь-яку кількість доданків
 ,
,
де  кореляційний момент величин
кореляційний момент величин 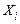 ,
, 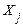 ; знак
; знак 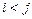 під знаком суми означає, що підсумовування поширюється на всі можливі попарні сполучення випадкових величин
під знаком суми означає, що підсумовування поширюється на всі можливі попарні сполучення випадкових величин 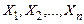 .
.
Якщо всі випадкові величини 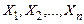 , що входять у систему, некорельовані (
, що входять у систему, некорельовані (  0 при
0 при  ), тоді
), тоді
 .
.
3. Математичне сподівання добутку двох випадкових величин дорівнює сумі добутку їхніх математичних сподівань і кореляційного моменту
 . (29)
. (29)
Доказ. Кореляційний момент по визначенню дорівнює
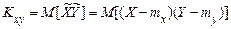 .
.
Використовуючи властивості математичного сподівання, отримаємо

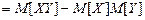 ,
,
що й було потрібно довести.
Математичне сподівання добутку двох некорельованих ( 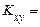 0) випадкових величин дорівнює добутку їхніх математичних сподівань
0) випадкових величин дорівнює добутку їхніх математичних сподівань
 .
.
Для довільної множини незалежних випадкових величин справедливо
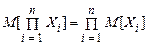 .
.
4. Дисперсія добутку двох незалежних випадкових величин
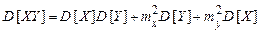 . (30)
. (30)
Доказ. Позначимо 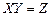 . По визначенню дисперсії
. По визначенню дисперсії
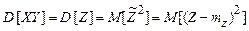 .
.
Величини  незалежні, тому
незалежні, тому  й
й
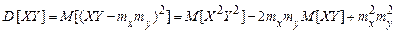 .
.
З урахуванням незалежності 
 ,
, 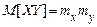 ,
,
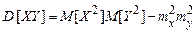 . (31)
. (31)
Другі початкові моменти виражаються через дисперсію
 ,
,  .
.
Підставивши ці вирази в (31) і привівши подібні, отримуємо (30).
Дисперсія добутку незалежних центрованих випадкових величин дорівнює добутку їхніх дисперсій
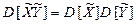 .
.
5. Математичне сподівання лінійної функції дорівнює тієї ж лінійної функції від математичних сподівань аргументів
 , (32)
, (32)
де  невипадкові коефіцієнти.
невипадкові коефіцієнти.
Доказ. Користуючись теоремою додавання математичних сподівань, отримуємо
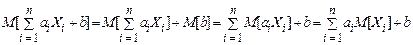 .
.
6. Дисперсія лінійної функції виражається формулою
 , (33)
, (33)
де  кореляційний момент величин
кореляційний момент величин 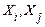 .
.
Доказ. Введемо позначення 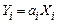 , тоді
, тоді
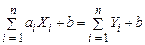 .
.
Застосовуючи формулу для дисперсії суми й з огляду на те, що  0, маємо
0, маємо
 , (34)
, (34)
де 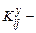 кореляційний момент величин
кореляційний момент величин 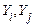 , що дорівнює
, що дорівнює 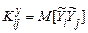 .
.
Оскільки 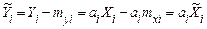 і, відповідно
і, відповідно 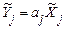 , то
, то
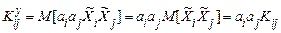 .
.
Підставляючи вираз для  в (34), приходимо до (33). У випадку, коли всі величини
в (34), приходимо до (33). У випадку, коли всі величини 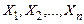 , що входять у систему, некорельовані (
, що входять у систему, некорельовані (  0 при
0 при  ), формула (33) набуває вид
), формула (33) набуває вид
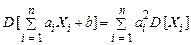 .
.
| <== попередня сторінка | | | наступна сторінка ==> |
| Числові характеристики векторних випадкових величин | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |