
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Числові характеристики векторних випадкових величин
Для наближеного опису системи двох випадкових величин, за аналогією зі скалярними величинами, можна ввести числові характеристики – початкові й центральні моменти різних порядків.
Початковим моментом порядку  системи двох випадкових величин
системи двох випадкових величин  і
і  називається математичне сподівання добутку
називається математичне сподівання добутку 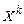 на
на 
 . (21)
. (21)
Центральним моментом порядку  системи двох випадкових величин
системи двох випадкових величин  і
і  називається математичне сподівання добутку
називається математичне сподівання добутку  го і
го і 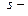 го ступенів відповідних центрованих величин
го ступенів відповідних центрованих величин
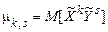 . (22)
. (22)
Для дискретних випадкових величин
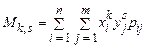 ,
,  ,
,
де 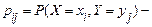 ймовірність того, що система двох випадкових величин
ймовірність того, що система двох випадкових величин  ,
,  прийме значення
прийме значення 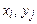 .
.
Для неперервних випадкових величин
 ,
,
 ,
,
де  спільна щільність імовірності двох випадкових величин
спільна щільність імовірності двох випадкових величин  ,
,  .
.
Особливу роль при описі системи випадкових величин грає другий змішаний центральний момент (математичне сподівання добутку центрованих значень випадкових величин)
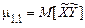 .
.
Цей момент називається кореляційним моментом («моментом зв'язку») випадкових величин  і
і  , має спеціальне позначення
, має спеціальне позначення 
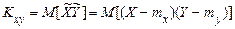 (23)
(23)
і характеризує ступінь статистичної залежності між  і
і  .
.
Необхідно відзначити принципову відмінність статистичної (ймовірнісної) залежності від функціональної (детермінованої).
Нехай, наприклад, до опору  прикладається постійна, але випадкова від досліду до досліду напруга
прикладається постійна, але випадкова від досліду до досліду напруга 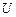 . Тоді струм через опір теж буде випадковою величиною, значення якої
. Тоді струм через опір теж буде випадковою величиною, значення якої 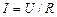 визначається законом Ома. Така залежність, коли кожному значенню однієї випадкової величини відповідає одне, цілком визначене, значення іншої випадкової величини, є функціональною залежністю між випадковими величинами.
визначається законом Ома. Така залежність, коли кожному значенню однієї випадкової величини відповідає одне, цілком визначене, значення іншої випадкової величини, є функціональною залежністю між випадковими величинами.
Статистична залежність характеризується тим, що в різних дослідах вона виявляється по-різному. При цьому тому самому значенню однієї випадкової величини можуть відповідати різні значення іншої випадкової величини. Прикладом статистичної залежності між двома випадковими величинами може бути залежність часу безвідмовної роботи радіостанції від часу, який витрачено на її технічне обслуговування, або залежність граничної дальності виявлення повітряного судна від потужності передавача радіолокаційної станції.
Для дискретних випадкових величин
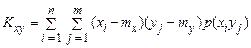 , (24)
, (24)
а для неперервних
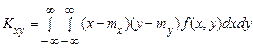 . (25)
. (25)
Доведемо, що для незалежних випадкових величин кореляційний момент дорівнює нулю.
Нехай 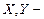 незалежні, наприклад неперервні, випадкові величини зі спільною щільністю ймовірності
незалежні, наприклад неперервні, випадкові величини зі спільною щільністю ймовірності 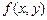 . Згідно з (20) для незалежних випадкових величин
. Згідно з (20) для незалежних випадкових величин
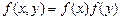 ,
,
де 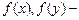 щільності ймовірності відповідно величин
щільності ймовірності відповідно величин  і
і  .
.
Підставляючи (20) в (25), одержимо добуток двох інтегралів
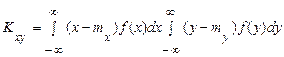
 .
.
Кожний із цих інтегралів являє собою перший центральний момент відповідної випадкової величини, що, по визначенню, дорівнює нулю. Отже, для незалежних неперервних випадкових величин 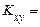 0. Для незалежних дискретних випадкових величин наведене положення доводиться аналогічно.
0. Для незалежних дискретних випадкових величин наведене положення доводиться аналогічно.
Таким чином, ознакою наявності залежності між випадковими величинами є відмінність від нуля значення  .
.
З формули (23) слідує, що  характеризує не тільки ступінь залежності величин, але і їхнє розсіювання. Дійсно, якщо, наприклад, одна з величин практично не відхиляється від свого математичного сподівання (є практично детермінованою), то
характеризує не тільки ступінь залежності величин, але і їхнє розсіювання. Дійсно, якщо, наприклад, одна з величин практично не відхиляється від свого математичного сподівання (є практично детермінованою), то 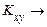 0 при будь-якому ступені статистичної залежності між
0 при будь-якому ступені статистичної залежності між  і
і  . Тому для характеристики винятково ступеня статистичної залежності між випадковими величинами переходять від моменту
. Тому для характеристики винятково ступеня статистичної залежності між випадковими величинами переходять від моменту  до коефіцієнта кореляції
до коефіцієнта кореляції 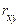 , що являє собою нормоване (безрозмірне) значення кореляційного моменту
, що являє собою нормоване (безрозмірне) значення кореляційного моменту
 , (26)
, (26)
де 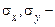 середні квадратичні відхилення відповідно
середні квадратичні відхилення відповідно  і
і  .
.
Випадкові величини, для яких 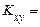 0 (а значить і
0 (а значить і  0), називаються некорельованими.
0), називаються некорельованими.
Нехай  і
і  пов'язані функціональною лінійною залежністю
пов'язані функціональною лінійною залежністю
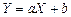 .
.
Покажемо, що в цьому випадку коефіцієнт кореляції  досягає свого найбільшого по модулю значення, рівного одиниці, а саме, якщо
досягає свого найбільшого по модулю значення, рівного одиниці, а саме, якщо  0, то
0, то  1, а якщо
1, а якщо 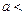 0, то
0, то 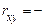 1 (негативна кореляція спостерігається у випадку, коли збільшення однієї з випадкових величин супроводжується зменшенням іншої).
1 (негативна кореляція спостерігається у випадку, коли збільшення однієї з випадкових величин супроводжується зменшенням іншої).
З функціональної лінійної залежності маємо  й, отже,
й, отже,  . Тому
. Тому  й
й 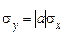 . Нарешті
. Нарешті
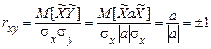 ,
,  .
.
Через те, що дляи незалежних  і
і  коефіцієнт кореляції дорівнює нулю, а свого найбільшого (по модулю) значення він досягає, якщо
коефіцієнт кореляції дорівнює нулю, а свого найбільшого (по модулю) значення він досягає, якщо  і
і  пов'язані лінійною залежністю, прийнято
пов'язані лінійною залежністю, прийнято 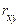 трактувати як міру лінійної статистичної залежностіміж
трактувати як міру лінійної статистичної залежностіміж  і
і  .
.
Оскільки коефіцієнт кореляції є мірою не всякої, а тільки лінійної залежності між  і
і  , можуть зустрічатися випадки, коли він звертається в нуль при залежних
, можуть зустрічатися випадки, коли він звертається в нуль при залежних  і
і  .
.
Наприклад, споживана потужність 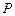 і напруга
і напруга 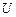 пов'язані відомою функціональною залежністю виду
пов'язані відомою функціональною залежністю виду
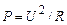 .
.
Припустимо, що напруга є випадковою величиною, щільність ймовірності якої 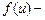 парна функція.
парна функція.
Очевидно, що  й
й  . Тому
. Тому
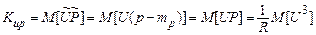 .
.
Виконуючи обчислення математичного сподівання, отримаємо
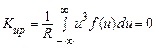 ,
,
тому що підінтегральна функція є непарною.
Отже, рівність нулю кореляційного моменту (коефіцієнта кореляції) – необхідна, але недостатня умова незалежності випадкових величин. З незалежності випадкових величин випливає їх некорельованість, а з некорельованості ще не слідує їхня незалежність.
| <== попередня сторінка | | | наступна сторінка ==> |
| ЛЕКЦІЯ 7 | | | ЛЕКЦІЯ 8 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |