
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ЛЕКЦІЯ 7
Спільна щільність ймовірності 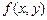 двох неперервних випадкових величин є така ненегативна функція, що добуток
двох неперервних випадкових величин є така ненегативна функція, що добуток 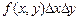 дорівнює ймовірності одночасного влучення
дорівнює ймовірності одночасного влучення  в інтервал
в інтервал 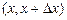 і
і  в інтервал
в інтервал 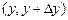 , тобто
, тобто
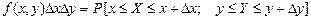 .
.
Геометрично щільності 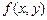 відповідає деяка поверхня в тривимірному просторі.
відповідає деяка поверхня в тривимірному просторі.
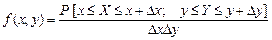 .
.
Якщо трактувати добуток 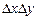 як елемент площі на площині змінних
як елемент площі на площині змінних  ,
,  , то щільність
, то щільність 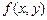 є кількість імовірності, що припадає на одиницю площі (рис. 6). Звідси, зокрема, слідує, що
є кількість імовірності, що припадає на одиницю площі (рис. 6). Звідси, зокрема, слідує, що 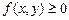 .
.
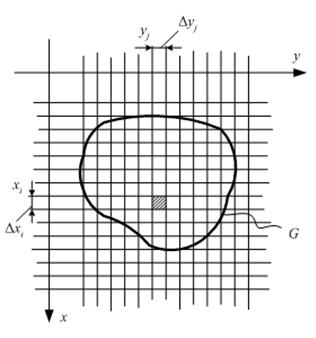
Рис.6. Пояснення переходу від системи двох неперервних випадкових величин до дискретних
Виконавши 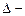 розбивку області змінних
розбивку області змінних 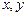 і розглядаючи неперервні величини як граничний випадок дискретних, можна одержати формули, аналогічні наведеним раніше. Наприклад,
і розглядаючи неперервні величини як граничний випадок дискретних, можна одержати формули, аналогічні наведеним раніше. Наприклад,
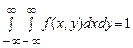 . (18)
. (18)
Ця формула є аналогом формули (13) і виражає властивість нормування спільної щільності ймовірності.
 .
.
Наведені формули виражають властивість погодженості щільностей ймовірності, відповідно до якої щільності ймовірності 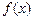 й
й 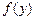 можна знайти, інтегруючи спільну щільність
можна знайти, інтегруючи спільну щільність 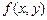 по «зайвій» змінній.
по «зайвій» змінній.
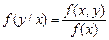 .
.
Ця формула випливає з формули (15). Умовна щільність ймовірності 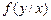 характеризує собою розподіл випадкової величини
характеризує собою розподіл випадкової величини  за умови, що деяке значення
за умови, що деяке значення 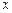 фіксоване. Її можна визначити як функцію
фіксоване. Її можна визначити як функцію 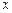 й
й 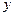 , що при множенні на
, що при множенні на  дає умовну ймовірність попадання
дає умовну ймовірність попадання  в інтервал
в інтервал 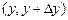 за умови, що випадкова величина
за умови, що випадкова величина  фіксована й дорівнює
фіксована й дорівнює 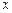 .
.
За аналогією з випадковими подіями, дві випадкові величини  й
й  називаються незалежними, якщо закон розподілу кожної з них не залежить від того, яке значення прийняла інша. У противному випадку величини
називаються незалежними, якщо закон розподілу кожної з них не залежить від того, яке значення прийняла інша. У противному випадку величини  й
й  називаються залежними.
називаються залежними.
Для неперервних випадкових величин умова незалежності  від
від  записується у вигляді
записується у вигляді
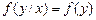 . (19)
. (19)
По теоремі множення щільностей ймовірностей з (19) отримуємо необхідну й достатню умову незалежності випадкових величин, що входять у систему
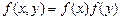 . (20)
. (20)
Приклад. Задана спільна щільність імовірності випадкових величин  і
і  . Потрібно встановити залежність (незалежність) випадкових величин
. Потрібно встановити залежність (незалежність) випадкових величин  і
і  .
.
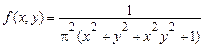 .
.
Розклавши знаменник на множники, маємо
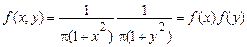 ,
,
де 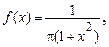
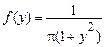 .
.
Тобто, відповідно до (20) випадкові величини  і
і  є незалежними.
є незалежними.
Для довільного числа випадкових величин закон розподілу їхньої системи (вектора) також задається функцією розподілу або спільною щільністю ймовірності.
Функцією розподілу системи 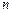 випадкових величин
випадкових величин 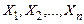 називається ймовірність спільного виконання
називається ймовірність спільного виконання 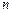 нерівностей виду
нерівностей виду 
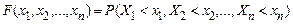 .
.
Спільною щільністю ймовірності системи 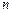 неперервних випадкових величин
неперервних випадкових величин 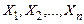 називається
називається 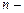 а змішана частинна похідна від функції
а змішана частинна похідна від функції 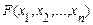 , яка узята один раз по кожному з аргументів
, яка узята один раз по кожному з аргументів
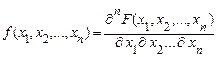 .
.
| <== попередня сторінка | | | наступна сторінка ==> |
| Закон розподілу векторної випадкової величини | | | Числові характеристики векторних випадкових величин |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |