• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Закон розподілу векторної випадкової величини

Для опису дискретної скалярної випадкової величини використовуєтьсяряд ймовірностей. За аналогією зі скалярною випадковою величиною, систему двох дискретних випадкових величин і , що приймають по кожній координаті кінцеве число значень, можна описати за допомогою таблиці (по типу ряду ймовірностей), у яку заносяться ймовірності спільного спостереження й .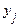

Оскільки в результаті досліду обов'язково спостерігається одна із сукупностей 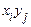( 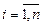; 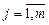), причому всі такі сполучення несумісні, то

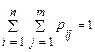(13)

Ця рівність відображає умову нормування спільних ймовірностей.

Нехай інтерес становить ймовірність прийняття деякого конкретного значення однією з випадкових величин, наприклад . З огляду на те, що може спостерігатися одночасно з однією з величин 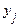, а всі такі варіанти несумісні, то на підставі теореми додавання ймовірностей отримуємо

. (14)

Розподіл випадкової величини , при обраному значенні іншої випадкової величини, слідує з теореми множення ймовірностей

. (15)

Умовна ймовірність так само, як безумовні ймовірності , , задовольняє умові нормування

.

Величина

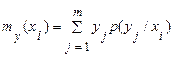( 16)

визначає середнє значення при 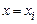й називається умовним математичним сподіванням при заданому значенні .

Безумовне математичне сподівання 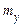знаходиться усередненням умовного математичного сподівання за всіма значеннями .

.

Аналогічні формули просто формально записати для 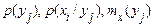. Так, наприклад

.

Імовірність сукупності 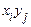прийняти значення з деякої області G, обумовленої співвідношеннями

,

визначається по формулі

.

За аналогією зі скалярними випадковими величинами, функцією розподілу системи двох випадкових величин і називається ймовірність спільного виконання двох нерівностей і 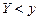, тобто

. ( 17)

Властивості функції розподілу системи двох випадкових величин.

1. Функція розподілу є неспадаючою функцією своїх аргументів

при ;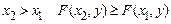

при .

2. Функція розподілу всюди на дорівнює нулю

.

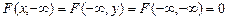3. При рівності однієї з випадкових величин 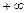, функція розподілу системи перетворюється у функцію розподілу іншої випадкової величини

.

4. Якщо обидва аргументи функції розподіли рівні 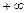, то

.

Функція розподілу системи визначена як для дискретних, так і для неперервних випадкових величин. Однак систему двох неперервних випадкових величин і звичайно задають спільною щільністю ймовірності.

Переглядів: 505