Моментні й кореляційні функції

Хоча вичерпний опис випадкового процесу дається багатомірними щільностями ймовірності (багатомірними функціями розподілу або багатомірними характеристичними функціями), у ряді випадків достатнім є знання інших, більш простих характеристик випадкового процесу. Це пояснюється декількома причинами.

По-перше, у багатьох задачах радіотехніки необхідно аналізувати перетворення випадкових процесів лінійними й нелінійними інерційними системами. Якщо з розгляду фізичної моделі джерела процесу отримані вирази для щільностей ймовірності, то, за винятком марківських процесів і лінійного перетворення нормальних процесів, не можна вказати метод безпосереднього перерахування щільностей ймовірності (функцій розподілу, характеристичних функцій) при інерційних перетвореннях випадкових процесів. Ця задача, як правило, вирішується приблизно шляхом перерахування окремих характеристик випадкового процесу, що дозволяє, у принципі, знайти щільність ймовірності для перетвореного процесу.

По-друге, у випадках, коли нам невідомий механізм пристрою, що формує процес, для з'ясування характеру випадкового процесу необхідно експериментально визначати відповідної щільності ймовірності. Експериментально порівняно просто можна визначити часткові характеристики процесу. Експериментальне ж визначення самих щільностей ймовірності у більшості практичних випадків виявляється трудомістким і дорогим. Тут виключення становить одномірна щільність ймовірності, для визначення якої є відповідні прилади. Однак вона не містить характеристик динаміки процесу, зазвичай необхідних для розв’язання практичних завдань.

У третіх, на практиці часто зустрічаються випадкові процеси, наприклад, що розподілені за нормальним законом, щільності ймовірності яких визначаються невеликою кількістю параметрів.

У четвертих, ряд практичних задач може бути успішно вирішений на основі розгляду окремих, часткових характеристик випадкового процесу. Якщо, наприклад, модульоване коливання діє на радіоприймальний пристрій з амплітудним детектором, то звичайно не цікавляться значенням початкової фази й розглядають лише відтворення закону модуляції.

Як характеристики випадкового процесу 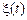більш прості, ніж щільності ймовірності, на практиці використовуються моментні й кореляційні функції. Їх корисною властивістю є те, що функції більш низького порядку несуть більше відомостей про випадковий процес, ніж функції високого порядку. Тому на практиці часто обмежуються розглядом лише декількох перших функцій.

Для випадкових процесів, як і для випадкових величин, розрізняють початкові й центральні моменти, які тут є функціями часу.

Під початковими моментними функціями випадкового процесу 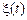, заданого на деякому інтервалі, розуміють симетричні щодо всіх своїх аргументів функції, що є математичними сподіваннями відповідних добутків

де невід'ємні цілі числа.

Моментна функція , що залежить від п незбіжних аргументів , називається п-мірною моментною функцією порядку 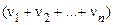. Так, одномірна моментна функція 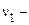го порядку, 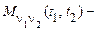двовимірна моментна функція порядку .

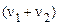Замість початкових моментних функцій можна розглядати центральні моментні функції, які, наприклад, для двовимірного випадку визначаються формулою

Відповідні моментні функції можна визначити також шляхом розкладання характеристичної функції в ряд Маклорена. Для одномірного випадку

. (15)

Формула (15) дає простий спосіб обчислення моментних функцій шляхом диференціювання характеристичної функції.

Справедливо й зворотне твердження, а саме, по відомим моментним функціям можна однозначно відновити характеристичну функцію

. (16)

Не приводячи громіздкі формальні викладення, укажемо формули, що встановлюють однозначний зв'язок моментних і кореляційних функцій

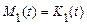Таким чином, моментні функції однозначно виражаються через кореляційні. По моментним або кореляційним функціям можна відновити характеристичну функцію й, отже, щільність ймовірності. Тому моментні функції так само, як і кореляційні, можуть бути використані для опису випадкових процесів.

Співвідношення між різними характеристиками випадкового процесу наведені на рис. 2. Заради простоти математичних записів рисунок відноситься до одномірного випадку, однак зображені взаємозв'язки справедливі й для багатомірного випадку.

Рис. 2 Співвідношення між характеристиками випадкового процесу

Оскільки моментні й кореляційні функції визначаються як коефіцієнти розкладання характеристичної функції в ряд Маклорена, то, природно, перші коефіцієнти відповідних розкладань є найбільш важливими й суттєвими. Надалі буде доведено особливу роль кореляційних функцій й .

Розділ теорії, присвячений вивченню властивостей випадкових процесів, які визначаються цими характеристиками, називається кореляційною теорією випадкових процесів. Кореляційна теорія дає повний (вичерпний) опис важливого класу нормальних випадкових процесів. Відправляючись від умовних щільностей ймовірності, можна ввести умовні моментні й умовні кореляційні функції. Вони визначаються аналогічними формулами, тільки тепер потрібно оперувати з умовними щільностями ймовірності й умовними характеристичними функціями.

Умовне математичне сподівання й умовна дисперсія для умовних щільностей ймовірності для однієї випадкової величини при фіксованих інших, визначаються відповідно формулами

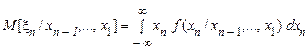, (17)

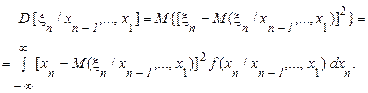(18)

<== попередня сторінка	\|	наступна сторінка ==>
ЛЕКЦІЯ 12	\|	ЛЕКЦІЯ 13

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.