Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ЛЕКЦІЯ 12

Введемо поняття умовної щільності ймовірності. Припустимо, що нам відоме значення процесу 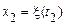. У загальному випадку знання 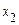дає також деяку інформацію про випадкову величину . Тепер випадкова величина буде мати щільність ймовірності

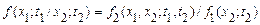, (9)

де .

Щільність ймовірності називається умовною щільністю ймовірності для при заданому значенні 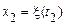. Умовна щільність імовірності повинна задовольняти умовам невід'ємності

(10)

і нормування

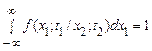. (11)

Умовна щільність ймовірності містить більше (принаймні не менше) відомостей про , чим безумовна щільність ймовірності . Наскільки саме збільшується інформація про у результаті того, що стало відомим значення 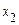, залежить від конкретних умов. У деяких випадках інформація про взагалі не додається, яким би не виявилося значення 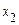. Це означає, що

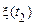При цьому не залежить від , а двовимірна щільність ймовірності дорівнює добутку одномірних щільностей ймовірності

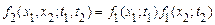. (12)

Рівність (12) виражає необхідну й достатню умову незалежності випадкових процесів.

Для реальних випадкових процесів, що спостерегаються у радіотехнічних системах з кінцевою «пам'яттю», умова незалежності (12) виконуються практично завжди при .

В іншому протилежному крайньому випадку, коли різниця 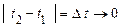(процес збігається із самим собою), маємо

і, отже,

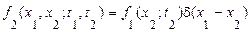де 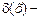дельта-функція.

Поняття умовної щільності ймовірності узагальнюється на багатомірні щільності ймовірності. З умовними щільностями ймовірності однозначно зв'язані відповідні умовні функції розподілу.

Приведемо два правила виключення «зайвих» аргументів з умовної щільності ймовірності. Назвемо аргументи, що знаходяться в умовній щільності ймовірності ліворуч від вертикальної риси «лівими», а праворуч – «правими».

1. Щоб з умовної щільності ймовірності виключити які-небудь «ліві зайві» аргументи, необхідно проінтегрувати у нескінченних межах умовну щільність ймовірності по цим «зайвим» змінним. Наприклад,

2. Для виключення «правих зайвих» змінних необхідно вихідну умовну щільність ймовірності помножити на умовну щільність ймовірності цих «зайвих» змінних при фіксованих інших «правих» змінних і отриманий результат проінтегрувати у нескінченних межах по «правим» змінним, що виключаються. Наприклад, для виключення двох «правих» змінних необхідно записати

Наведені результати справедливі й при розгляді дискретних випадкових величин. У цьому випадку потрібно замінити умовні щільності ймовірності на відповідні ймовірності, а інтеграли – на суми. Наприклад, якщо дискретні випадкові величини 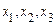приймають відповідно значення , то

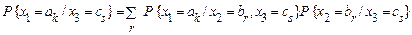Для опису випадкового процесу, поряд із щільностями ймовірності, можна використовувати характеристичні функції.

Характеристичною функцією випадкового процесу називається перетворення Фур'є від відповідної щільності ймовірності

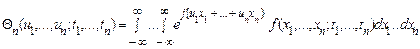де 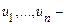дійсні змінні.

Звідси випливає, що характеристичну функцію можна також визначити як математичне сподівання експоненти

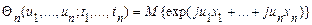При оцінці доцільності застосування характеристичних функцій для опису випадкових процесів необхідно враховувати два важливих результати:

1. Спільна характеристична функція незалежних випадкових величин дорівнює добутку характеристичних функцій окремих величин.

2. Характеристична функція суми взаємно незалежних випадкових величин дорівнює добутку характеристичних функцій доданків.

Для характеристичних функцій також справедлива умова симетрії, а умови нормування й узгодженості відповідно мають вигляд:

, (13)

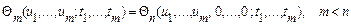. (14)

Рівність (14) означає, що з характеристичної функції 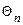можна завжди одержати характеристичну функцію 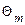меншої мірності (т<п), поклавши рівними нулю «зайві» аргументи 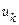. У цьому полягає ще одна перевага оперування з характеристичними функціями в порівнянні із щільностями ймовірності.

<== попередня сторінка	\|	наступна сторінка ==>
Функції розподілу й щільності ймовірності	\|	Моментні й кореляційні функції

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.