Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Функції розподілу й щільності ймовірності

Припустимо, що є велике число 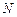повністю ідентичних систем, що працюють одночасно й в однакових умовах. На виході цих систем спостерігається випадковий процес 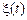. Якщо до кожної системи підключити однакові прилади реєстації (наприклад, осцилографи) і на всіх приладах у тий самий час 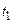зафіксувати вихідні миттєві значення, то одержимо 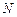величин , що відрізняються одна від іншої.

Виділимо із загального числа N ті величин, значення яких у момент часу 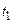менше або дорівнюють заданому числу 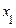. При досить великому N відносна частка 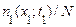величин, що задовольняють цій умові, буде мати статистичну усталеність (групуватися біля деякого постійного числа) і може розглядатися як ймовірність того, що при 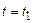випадкова функція 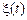не перевищує значення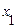

. (1)

Функція називається одномірною функцією розподілу ймовірностей і описує значення випадкової функції в один, фіксований момент часу.

Похідна від функції розподілу ймовірностей

(2)

називається одномірною щільністю ймовірності випадкового процесу. Безрозмірна величина являє собою ймовірності того, що випадкова величина 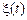буде укладена а в інтервалі

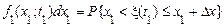. (3)

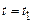Одномірна щільність ймовірності й одномірна функція розподілу дають уявлення про процес лише в один, фіксований момент часу, не вказуючи, наприклад, як значення в момент часу впливають на подальше поводження процесу при . Одномірні ймовірнісні характеристики описують процес статично й не дають уявлення про динаміку його розвитку.

Більш повними характеристиками випадкового процесу є двовимірна функція розподілу ймовірностей і двовимірна щільність імовірності, які відображають ймовірнісний зв'язок між значеннями процесу у два моменти часу й .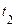

Двовимірна функція розподілу ймовірностей і двовимірна щільність ймовірності визначаються аналогічно одномірним. Вернемося знову до N ідентичних систем. Зробимо реєстрацію вихідних значень процесу у два моменти часу й 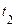. Нехай отримані значення в ці два моменти часу

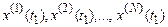й .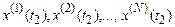

Підрахуємо відносну частку значень , які в момент часу не перевищують величини 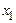й у момент часу 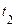не перевищують величини . Тоді для досить великого числа N функція

(4)

являє собою двовимірну функцію розподілу ймовірностей.

Похідна від цієї функції

(5)

називається двовимірною щільністю ймовірності.

Безрозмірна величина 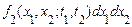являє собою ймовірність спільного виконання двох нерівностей 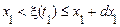й , тобто

. (6)

В (6) права частина при великих N являє собою відносну частку значень , які в момент часу попадають в інтервал і в момент часу в інтервал .

Двовимірні функція розподілу й щільність ймовірності часто використовуються в практичних розрахунках, однак вони також не забезпечують вичерпного опису випадкового процесу, оскільки дозволяють судити про зв'язок між ймовірними значеннями випадкового процесу лише у два моменти часу.

Повний опис випадкового процесу дається багатомірною щільністю ймовірності (функцію розподілу) ймовірності , яка визначає ймовірність того, що значення випадкового процесу 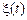в п моментів часу укладені у відповідних малих інтервалах . Ця ймовірність дорівнює

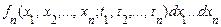Щільність імовірності дозволяє судити про зв'язок між ймовірними значеннями процесу в п довільно взятих моментів часу.

Таким чином, випадковий процес у загальному випадку описується за допомогою п-мірної щільності ймовірності (функції розподілу) і тим детальніше, чим більше п. Два випадкових процеси, у яких всі кінцевомірні функції розподілу збігаються, називаються еквівалентними.

Функції розподілу ймовірностей і щільності ймовірності зв'язані однозначною залежністю:

де .

Тому для заданого n вони містять однакову інформацію про випадковий процес. При розгляді неперервних процесів оперують із щільностями ймовірності, які дають наочне уявлення про характер процесу. Щодо дискретних послідовностей, дискретних, неперервнозначних і змішаних процесів, щільності ймовірності яких мають розриви, необхідно переходити до функцій розподілу ймовірностей.

Щільності ймовірності випадкових процесів повинні задовольняти наступним чотирьом умовам:

1) умові від'ємності

; (7)

2) умові нормування

; (8)

3) умові симетрії, яка полягає в тому, що функції повинні бути симетричні щодо будь-яких перестановок всіх пар аргументів , оскільки ймовірність спільного здійснення п нерівностей не залежить від того, у якому порядку перелічувати ці нерівності;

4) умові узгодженості, що означає, що при будь-якому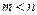

З умови узгодженості витікає, що, якщо відома п-мірна щільність ймовірності , то шляхом інтегрування її по «зайвим» аргументах легко знаходяться усі щільності ймовірності меншої кратності. У цьому зв'язку можна відзначити, що вичерпним був би опис випадкового процесу однією щільністю ймовірності максимального порядку. Внаслідок неперервності аргументу 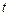, такого кінцевого максимального порядку в загальному випадку не існує. Відомі тільки два дуже важливих класи випадкових процесів, для яких всі п-мірні щільності ймовірності , , 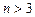математично строго виражаються через двовимірні щільності ймовірності 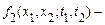це нормальні процеси й марківські процеси.

<== попередня сторінка	\|	наступна сторінка ==>
Опис випадкових процесів	\|	ЛЕКЦІЯ 12

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.