Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Стаціонарні й нестаціонарні процеси

Важливим класом випадкових процесів є стаціонарні випадкові процеси. Випадковий процес 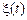називаєтьсястаціонарним у вузькому (строгому) сенсі, якщо його ймовірнісні характеристики не змінюються при будь-якому зсуві початку відліку часу. Це означає, що два процес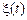и й 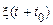мають однакові ймовірнісні характеристики при будь-якому значенні 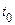. Випадкові процеси, що не задовольняють цій умові, називаються нестаціонарними.

З наведеного визначення слідує, що процес 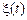є стаціонарним у вузькому сенсі, якщо його щільності ймовірності довільного порядку п не змінюються при будь-якому зсуві всієї групи відліків уздовж осі часу, тобто при будь-яких п і 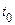справедлива рівність

Аналогічна рівність повинна виконуватися для функцій розподілу ймовірностей, а також для характеристичних, моментних і кореляційних функцій.

Стаціонарний процес, на відміну від нестаціонарного, поводиться однорідно (одноманітно) у часі (рис.3).

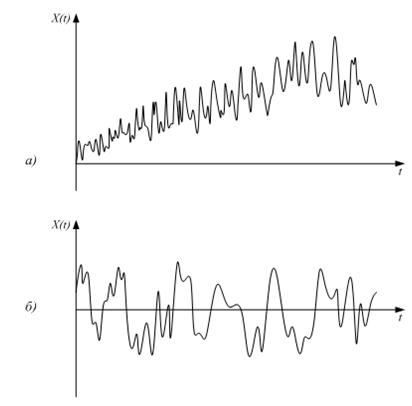
Рис.3 Реалізації нестаціонарного (а) й стаціонарного (б) випадкових процесів

Стаціонарні випадкові процеси, аналогічно детермінованим процесам, спостерігаються у сталому режимі роботи системи при незмінних зовнішніх умовах. Стаціонарні процеси є частковим випадком більш широкого класу нестаціонарних процесів. Прикладом нестаціонарного випадкового процесу може бути будь-який випадковий процес у перехідному режимі роботи системи (наприклад, випадковий процес на виході інерційної системи в початковий період роботи).

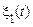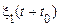Поняття стаціонарності узагальнюється на два й кілька випадкових процесів. Говорять, що два процеси і є спільно стаціонарними у вузькому сенсі, якщо спільні характеристики цих процесів такі ж, як і аналогічні характеристики для процесів і 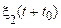при кожному 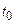. Відзначимо, що якщо кожний із процесів і сам по собі є стаціонарним, то звідси зовсім не слідує, що вони будуть спільно стаціонарними.

З визначення стаціонарності, зокрема, слідує

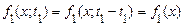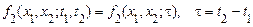Таким чином, для стаціонарного у вузькому сенсі випадкового процесу п-мірна щільність імовірності, п-мірні моментні й кореляційні функції залежать не від п, авід ( ) моментів часу, тому що один з обраних моментів часу можна завжди прийняти за початок відліку часу (наприклад, покласти ).

Одномірна щільність ймовірності стаціонарного в узькому сенсі процесу взагалі не залежить від часу. Тому одномірна щільність імовірності й одномірні моментні функції не враховують часових характеристик стаціонарного процесу: процес, що протікає в s разів швидше або повільніше, буде мати ту саму одномірну щільність ймовірності. Опис випадкового процесу за допомогою одномірної щільності ймовірності подібний завданню лише амплітуди гармонійного коливання без його частоти. Це ще раз підтверджує той факт, що опис випадкового процесу за допомогою одномірної щільності ймовірності є неповним.

Для підкреслення стаціонарності випадкового процесу будемо позначати його моментні й кореляційні функції малими літерами.

Очевидно, що математичне сподівання (середнє значення) стаціонарного процесу не залежить від часу

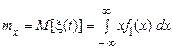. (19)

Двовимірна кореляційна функція залежить тільки від різниці аргументів 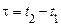і визначається формулою

(20)

Дисперсія стаціонарного процесу постійна й дорівнює значенню кореляційної функції при нульовому значенні аргументу

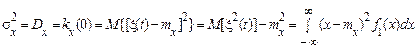При вирішенні багатьох практичних задач радіотехніки достатньо оперувати тільки з математичним сподіванням і кореляційною функцією випадкових процесів. У зв'язку із цим вводиться поняття слабкої стаціонарності або стаціонарності в широкому сенсі.

Випадковий процес 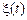називається стаціонарним у широкому сенсі (або слабко стаціонарним), якщо його математичне сподівання постійно (тобто не залежить від часу), а кореляційна функція залежить тільки від різниці аргументів :

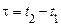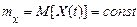, (21)

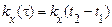. (22)

З формул (21), (22) слідує, що випадкові процеси, стаціонарні у вузькому сенсі, завжди стаціонарні в широкому сенсі. Однак зворотне твердження невірно.

Два процес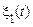и й називаються спільно стаціонарними в широкому сенсі, якщо кожний з них є стаціонарним у широкому сенсі й взаємна кореляційна функція між ними залежить тільки від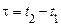

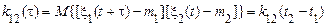Приклад. Нехайзаданий випадковий процес

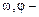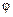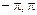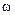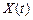де постійна величина, незалежні випадкові величини, причому рівномірно розподілена в інтервалі [ ], a має щільність імовірності . Покажемо, що процес є стаціонарним у широкому сенсі.

Визначимо математичне сподівання процесу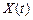

Визначимо кореляційну функцію

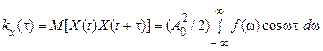Оскільки математичне сподівання процесу 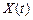дорівнює нулю, а кореляційна функція залежить тільки від 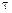, тому процес 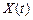є стаціонарним у широкому сенсі.

<== попередня сторінка	\|	наступна сторінка ==>
ЛЕКЦІЯ 13	\|	Ергодичні стаціонарні процеси

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.