• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Спектральні характеристики випадкового процесу

При розгляді детермінованих сигналів, розглянутих раніше, і реакції на них лінійних систем з постійними параметрами широко використовуються спектральні представлення, що базуються на можливості представлення сигналів рядом або інтегралом Фур'є. При цьому математично порівняно просто можна знайти сигнал на виході лінійної системи шляхом простого перерахування окремих спектральних складових вхідного сигналу через частотну характеристику лінійної системи з наступним застосуванням принципу суперпозиції. Представляється природним бажання поширити гармонічний аналіз й на випадкові процеси.

Енергетичний спектр стаціонарного в широкому сенсі випадкового процесу 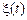визначається як перетворення Фур'є від кореляційної функції :

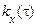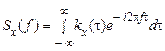. (34)

Щоб це перетворення існувало, передбачається, що кореляційна функція є абсолютно інтегруємою, тобто

.

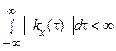На підставі зворотного перетворення Фур'є можемо записати

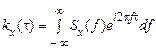. (35)

Таким чином, енергетичний спектр і кореляційна функція стаціонарного процесу, як й для детермінованих сигналів, являють собою пару взаємних перетворень Фур'є і називаються формулами Вінера-Хінчина.

Зі формул (34) і (35), відповідно при й 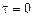, одержуємо

. (36)

Нагадаємо, що якщо під 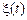розуміти випадковий (флуктуаційний) струм або напругу, то величина буде мати розмірність енергії. Цим і пояснюється назва «енергетичний спектр». Дисперсія («повна енергія») стаціонарного випадкового процесу дорівнює площі під кривою енергетичного спектра. Розмірну величину можна розглядати як частку енергії, що знаходиться у малому інтервалі частот .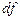

У такому випадку, якщо на вхід лінійної системи з безрозмірною передаточною функцією 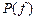впливає стаціонарний у широкому сенсі випадковий процес 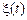ізенергетичним спектром , то енергетичний спектр процесу 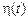на виході в стаціонарному режимі визначається простою формулою

. (37)

Перелічимо основні властивості енергетичного спектра стаціонарного випадкового процесу.

1. Енергетичний спектр стаціонарного процесу – невід'ємна величина:

.

Якщо допустити, що 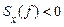в деякій смузі частот, то дисперсія вихідного процесу повинна бути від'ємною, що неможливо.

2. Енергетичний спектр стаціонарного в широкому сенсі випадкового процесу є парна функція частоти. Кореляційна функція 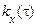такого процесу є парна функція аргументу, тому

.

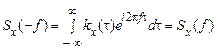З огляду на парність енергетичного спектра, формули для й 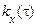можна спростити:

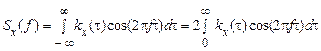, (38)

. (39)

3. Кореляційна функція й енергетичний спектр стаціонарного в широкому сенсі випадкового процесу мають всі властивості, характерні для пари взаємних перетворень Фур'є. Зокрема, чим «ширше» спектр, тим «уже» кореляційна функція, і навпаки, що виражається у вигляді відомого принципу або співвідношення невизначеності.

На відміну від двостороннього («математичного») спектра, що визначений для позитивних і від'ємних значень частоти, можна також розглядати однобічний («фізичний») спектр, відмінний від нуля лише при позитивних частотах

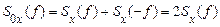. (40)

Тоді формули Вінера-Хінчина для приймають вид

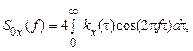(41)

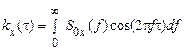. (42)

Для скорочення математичних виразів часто використовуються формули Вінера-Хінчина в наступному вигляді

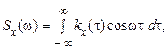(43)

. (44)

В інженерній практиці «довжина» енергетичного спектра по частоті характеризується ефективною шириною спектра

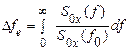, (45)

де значення енергетичного спектра при деякій характерній частоті. Зазвичай за 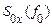беруть максимум енергетичного спектра або ординату, що відповідає точці симетрії. Іноді вказують ширину енергетичного спектра на рівні 0,5 .

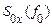При якісному розгляді характеру енергетичних спектрів можна виділити два класи: спектри, значення яких помітно відмінні від нуля тільки у вузькій смузі частот , щільно сконцентрованої біля частоти 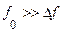, та спектри, що не задовольняють цій умові.

Стаціонарний випадковий процес, енергетичний спектр якого сконцентрований у вузькій смузі біля частоти

,

за аналогію з детермінованими процесами називається вузькосмуговим випадковим процесом. Якщо ця нерівність не виконується, то процес не є вузькосмуговим.

Замість енергетичного спектра можна розглядати нормований до одиниці енергетичний спектр

,

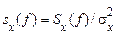який у літературі часто називають спектральною щільністю, оскільки 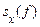має деякі властивості щільності ймовірності (вона ненегативна й нормована до одиниці).

Необхідно мати на увазі, що, на відміну від спектрального аналізу детермінованих сигналів, енергетичний спектр випадкового процесу не дає можливості відновити конкретну реалізацію процесу, тому що він не містить відомостей про фази окремих спектральних складових. Крім того, можна вказати різні за характером випадкові процеси, що мають однаковий енергетичний спектр і кореляційну функцію. Тому ці дві характеристики описують випадковий процес явно неповно.

Аналогічно енергетичному спектру одного процесу визначається взаємний енергетичний спектр двох стаціонарно зв'язаних у широкому сенсі випадкових процесів,як пряме перетворення Фур'є від взаємних кореляційних функцій.

Переглядів: 989