• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

ЛЕКЦІЯ 14

Конкретизуємо властивості кореляційних функцій щодо стаціонарного (хоча б у широкому сенсі) випадкового процесу.

1. Кореляційна функція стаціонарного процесу є парною функцією свого аргументу

. (30)

Дійсно, вираз для кореляційної функції стаціонарного процесу не залежить від вибору початку відліку часу.

2. Абсолютне значення кореляційної функції при кожному 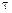не може перевищувати її значення при 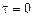, тобто

. (31)

Цей результат слідує з очевидної нерівності, що відбиває той факт, що математичне сподівання позитивної функції не може бути негативною величиною:

3. Якщо кореляційна функція неперервна при 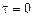, то вона неперервна при всіх інших значеннях .

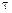4. Для стаціонарних випадкових процесів, що зустрічаються на практиці, справедливе співвідношення

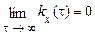, (32)

свідомо гарантуюче ергодичність процесу щодо математичного сподівання.

Фізично цей результат пояснюється тим, що реальні системи звичайно мають кінцевий час загасання (кінцевий час «пам'яті»). Тому для випадкових процесів, що спостерігаються у стаціонарно й стійко працюючих системах, наступне значення процесу виявляється практично незалежним і некорельованим з попереднім значенням, якщо вони розділені досить великим інтервалом часу.

Таким чином, кореляційна функція стаціонарного випадкового процесу є парною функцією аргументу 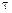, має максимум, рівний дисперсії при 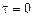, неперервна при всіх 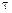, якщо тільки неперервна при 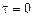, і, як правило, убуває до нуля при .

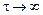Покажемо роль математичного сподівання, дисперсії й кореляційній функції в задачі оцінки випадкових величин. Припустимо, що потрібно знайти таку оцінку 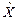випадкової величини , що мінімізує середній квадрат похибки

.

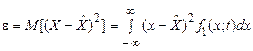Розписавши ліву частину цієї рівності, маємо

.

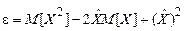Дорівнявши похідну по 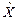нулю, знаходимо

.

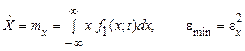Отже, математичне сподівання є найкращою оцінкою випадкової величини за критерієм мінімуму середнього квадрата похибки, причому мінімальне значення цієї похибки дорівнює дисперсії.

Для двох випадкових величин і 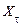найкращою оцінкою відповідно є умовне математичне сподівання 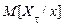при фіксованому .

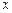В інженерній практиці замість точного аналітичного завдання коефіцієнта кореляції часто обмежуються зазначенням лише часу кореляції 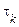, що дає орієнтовне уявлення про те, на якому інтервалі часу в середньому має місце помітна корельованість між значеннями випадкового процесу. Аналогічно тому, як оцінюється тривалість імпульсу, час кореляції можна визначити по-різному. Так, під часом кореляції 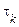можна розуміти величину

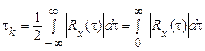. (33)

Геометрично 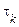дорівнює основі прямокутника з висотою 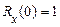, що має ту ж площу, що й площа, яка укладена між кривою при 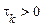й віссю абсцис.

Приклад. Розглянемо кореляційну функцію періодичного процесу, що формується сигналом виду 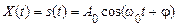, де 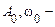постійні величини, 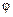рівномірно розподілена в інтервалі [ 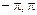] і має щільність імовірності 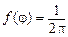при .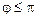

Кореляційна функція сигналу дорівнює

.

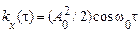У цьому випадку кореляційна функція виявляється періодичною й має той же період 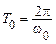, що й вихідний сигнал. На відміну від стаціонарних випадкових процесів, що часто зустрічаються, у цьому випадку кореляційна функція при 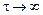не прагне до нуля. Цей факт використовується для виявлення й виділення досить довгого, але слабкого сигналу на фоні інтенсивної завади, що представляє собою випадковий процес.

Дійсно, нехай сигнал 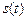приймається на фоні стаціонарної завади , тобто спостереженню доступний лише сумарний процес

.

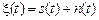Якщо сигнал і завада незалежні, то кореляційна функція сумарного процесу дорівнює сумі кореляційних функцій доданків

.

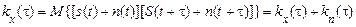Кореляційну функцію завади при 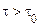практично можна вважати рівною нулю. Тому при 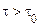. Отже, відповідь на питання про наявність або відсутність у прийнятому коливанні 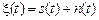гармонійного сигналу 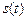можна одержати з аналізу кореляційної функції 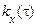. Якщо при досить більших 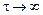вона є періодичною функцією, то це є ознакою того, що в 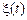є присутнім сигнал, і навпаки.

Кореляційна обробка сигналів, яку засновано на формуванні кореляційної функції випадкових процесів і реєстрації її значення, у багатьох радіотехнічних задачах є оптимальною (найкращої за обраним критерієм).

Переглядів: 570