Нормальний випадковий процес

При розгляді методів опису випадкових процесів вказувалося, що послідовність щільностей ймовірностей являє собою своєрідну ієрархічну градацію: з зростанням мірності 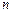вони описують випадковий процес усе більш й більш детально.

Складність опису випадкових процесів, тобто найбільший порядок 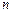-мірної щільності ймовірності, що дає повний опис випадкового процесу, можна покласти в основу класифікації випадкових процесів. Очевидно, найпростішим класом є випадкові процеси, повний опис яких досягається зазначенням одномірної щільності ймовірності ; наступним класом є процеси, вичерпний опис яких дається двовимірною щільністю ймовірності тощо. Нормальні випадкові процеси належать до другого класу: вичерпний опис таких процесів дається двовимірною щільністю ймовірності.

Нормальні випадкові процеси найбільш часто зустрічаються на практиці й тому займають особливе становище серед інших випадкових процесів. Це пояснюється тим фактом, що більшість випадкових процесів, що зустрічаються в радіотехніці, таких, наприклад, як теплові флуктуації, власний шум радіоприймача, атмосферні й космічні шуми, являють собою результуючий ефект (суму) великого числа порівняно слабких елементарних збурювань, що виникають у випадкові моменти часу. А відповідно до центральної граничної теореми теорії ймовірностей, що розглядалась раніше, щільність ймовірності суми елементарних збурювань зі збільшенням числа доданків необмежено наближається до нормальної, незалежно від того, які щільності ймовірності мають окремі доданки. При цьому важливо лише, щоб вплив окремих доданків на суму був рівномірно малим (приблизно однаковим).

Приведемо визначення нормального (гауссівcького) випадкового процесу. Дійсний випадковий процес 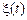називається нормальним (гауссівським), якщо для будь-якої кінцевої множини моментів часу випадкові величини 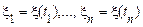є спільно нормальними, тобто мають нормальну (гауссівську) щільність ймовірності виду

Оскільки тут випадкові величини залежать від обраного моменту часу 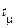, то для мірності щільності ймовірності доцільно зберегти позначення 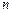,а для математичних сподівань, дисперсій і кореляційних функцій увести індекси .

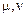Тому у виразі для нормального процесу: 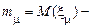математичне сподівання випадкової величини ; 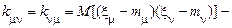кореляційний момент між випадковими величинами й 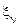( 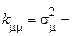дисперсія випадкової величини ); 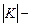визначник матриці

алгебраїчне доповнення елемента 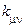у визначнику . Кореляційна матриця є симетричною, тобто .

Приведемо основні властивості нормального випадкового процесу.

1. З виразу для нормального випадкового процесу видно, що у формулу для щільності ймовірності входять тільки математичне сподівання й кореляційна функція. Якщо з фізичних міркувань відомо, що випадковий процес є нормальним, то він вичерпним образом визначається зазначенням закону зміни в часі математичного сподівання й кореляційної функції. Отже, кореляційна теорія дає повний опис нормальних процесів.

2. Для нормальних процесів всі кореляційні функції, починаючи з , дорівнюють нулю. Тому нормальні процеси можуть відрізнятися один від іншого тільки значенням математичного сподівання й видом кореляційної функції (енергетичного спектра).

3. Якщо значення випадкового процесу некорельовані, то вони й незалежні. У цьому випадку 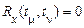при й 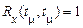, тому вираз для щільності ймовірності приймає вид

4. Для гауссівських випадкових процесів поняття стаціонарності в широкому й вузькому сенсі збігаються.

Припустимо, що виконуються співвідношення

тобто математичне очікування не залежить від вибору моменту часу і є постійним, а кореляційна функція залежить лише від значення інтервалу між розглянутими моментами часу. Тоді, по визначенню, нормальний процес буде стаціонарним у широкому сенсі. Однак він буде одночасно стаціонарним і в вузькому сенсі, тому що при цьому щільності ймовірності не будуть змінюватися при будь-якому зсуві всієї щільності уздовж осі часу на довільну постійну величину. При цьому п-мірна щільність ймовірності нормального стаціонарного процесу залежить тільки від (п—1) моментів часу, тому що один з розглянутих моментів часуможна взяти за початок відліку.

5. При лінійних перетвореннях нормальних випадкових процесів (сигналів) властивість нормальності зберігається. Якщо на вхід лінійної системи впливає нормальний випадковий процес, то процес на виході системи буде також нормальним. Тому говорять, що нормальні процеси мають властивість стійкості стосовно лінійних перетворень.

6. При нелінійних перетвореннях властивість нормальності втрачається. Зокрема, у результаті перемножування двох нормальних процесів нормальний процес не утворюється.

Однак, якщо ненормальний випадковий процес із часом кореляції 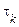впливає на інерційну лінійну систему (з постійною часу 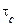), то процес на виході такої системи наближається до нормального (має місце нормалізація). Це наближення тим краще, чим сильніше виконується нерівність .

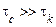<== попередня сторінка	\|	наступна сторінка ==>
	\|	Білий шум і його моделі

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.