
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Білий шум і його моделі
Розглянемо стаціонарний випадковий процес  , кореляційна функція якого дорівнює дельта-функції, помноженої на деяку постійну величину
, кореляційна функція якого дорівнює дельта-функції, помноженої на деяку постійну величину 
 . (46)
. (46)
Нагадаємо, що дельта-функція дорівнює нулю всюди, за винятком точки 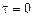 , де
, де 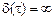 , причому інтеграл від дельта-функції на будь-якому інтервалі, що містить особливу точку
, причому інтеграл від дельта-функції на будь-якому інтервалі, що містить особливу точку 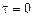 , дорівнює одиниці. Звідси слідує, що розглянутий випадковий процес характеризується тим, що його значення в будь-які два незбіжні, але як завгодно близькі, моменти часу, некорельовані. Такий процес, щоумовно можна вважати абсолютно випадковим процесом, називається білим гауссівським шумом.
, дорівнює одиниці. Звідси слідує, що розглянутий випадковий процес характеризується тим, що його значення в будь-які два незбіжні, але як завгодно близькі, моменти часу, некорельовані. Такий процес, щоумовно можна вважати абсолютно випадковим процесом, називається білим гауссівським шумом.
Енергетичний спектр білого гауссівського шуму
 , (47)
, (47)
постійний при всіх частотах. Рівномірність спектра в дуже широкому діапазоні частот і визначає назву білого шуму за аналогією з білим світлом, що має у видимій частині рівномірний спектр.
Для білого шуму має місце фізично неправдоподібний результат: дисперсія (середня потужність) такого шуму 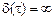 й для нього не можна аналітично записати навіть одномірну щільність ймовірності. Цей результат пояснюється тим, що білий шум варто розглядати як математичну модель, тому що реальні процеси завжди мають енергетичний спектр, що убуває при дуже високих частотах, і, отже, мають кінцевий час кореляції
й для нього не можна аналітично записати навіть одномірну щільність ймовірності. Цей результат пояснюється тим, що білий шум варто розглядати як математичну модель, тому що реальні процеси завжди мають енергетичний спектр, що убуває при дуже високих частотах, і, отже, мають кінцевий час кореляції 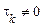 й обмежену середню потужність.
й обмежену середню потужність.
Білий шум є корисною математичною ідеалізацією, яка застосовується в тих випадках, коли в межах амплітудно-частотної характеристики радіотехнічної системи енергетичний спектр зовнішнього реального шуму можна приблизно вважати постійним або, інакше, коли час кореляції шуму багато менше всіх постійних часу системи, на яку впливає шум.
У якості конкретних фізичних прикладів флуктуаційних шумів, які часто розглядають як моделі білого шуму, можна вказати дробовий шум електронних приладів і тепловий шум резисторів.
У радіотехніці часто зустрічаються задачі аналізу впливу шуму з досить широким плавним енергетичним спектром на порівняно інерційні («вузькосмугові») системи. З метою спрощення вирішення ряду подібних задач, не роблячи при цьому великої помилки, реальний широкосмуговий шум, що впливає, можна заміняти на «еквівалентний» білий шум.
Можна вказати наступну наближену умову й правило заміни реального процесу (шуму) на білий шум. Нехай розглядається вплив на деяку систему з постійної часу 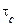 реального стаціонарного шуму зкореляційною функцією
реального стаціонарного шуму зкореляційною функцією 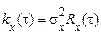 , яка характеризується досить широким спектром
, яка характеризується досить широким спектром  і, отже, малим, але кінцевим часом кореляції
і, отже, малим, але кінцевим часом кореляції  . У цьому випадку реальний шум можна розглядати як білий шум. За значення енергетичного спектра «еквівалентного» білого шуму можна взяти значення
. У цьому випадку реальний шум можна розглядати як білий шум. За значення енергетичного спектра «еквівалентного» білого шуму можна взяти значення  , що дорівнює
, що дорівнює
 .
.
Іноді надходять навпаки: граничний перехід до білого шуму здійснюють не на початковій стадії аналізу, а в кінцевих результатах. При цьому як моделі реальних процесів, що дозволяють найбільш просто здійснити такий перехід, часто розглядають стаціонарні випадкові процеси із двома видами кореляційних функцій

Варто пам'ятати, що дельта-функція має розмірність, зворотну розмірності аргументу.
Для аналізу й синтезу сучасних цифрових радіосистем, що описуються у дискретному часі, потрібне введення дискретного білого шуму. Тоді приймається, що дискретний шум  формується з неперервного
формується з неперервного  за допомогою згладжування за елементарний інтервал часу
за допомогою згладжування за елементарний інтервал часу  й
й
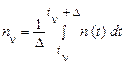 . (48)
. (48)
При цьому під дискретним білим шумом розуміється послідовність {  } незалежних гауссівських випадкових величин з нульовим математичним сподіванням
} незалежних гауссівських випадкових величин з нульовим математичним сподіванням  і однаковою дисперсією
і однаковою дисперсією  . Всі значення дискретного білого шуму мають ту саму нормальну щільність ймовірності
. Всі значення дискретного білого шуму мають ту саму нормальну щільність ймовірності
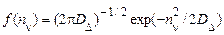 . (49)
. (49)
| <== попередня сторінка | | | наступна сторінка ==> |
| Нормальний випадковий процес | | | Марківські випадкові процеси |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |