
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Коефіцієнт кореляції Спірмена
Для оцінки сили зв’язку між Х та Y у випадку, коли між Х та Y існує нелінійний зв’язок або вибіркові дані не розподілені за нормальним законом, слугує коефіцієнт кореляції Спірмена.
Коефіцієнт кореляції Спірмена розраховується за формулою:
 , (3.5)
, (3.5)
де п – кількість пар вибіркових даних;
 – різність між рангами і-го значення Х та відповідного значення Y;
– різність між рангами і-го значення Х та відповідного значення Y;
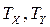 – поправки, що пов’язані з однаковими рангами; розраховуються за формулами:
– поправки, що пов’язані з однаковими рангами; розраховуються за формулами:
 ;
; 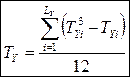 , (3.6)
, (3.6)
де  – кількість зв’язок (груп однакових рангів);
– кількість зв’язок (груп однакових рангів);
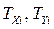 – розміри і-тих зв’язок (кількість елементів в них).
– розміри і-тих зв’язок (кількість елементів в них).
Зауваження 1. Ранги присвоюються вибірковим даним звичайним способом (див. п. 2.3.4).
Зауваження 2. Статистична значущість коефіцієнта кореляції Спірмена перевіряється так, як й коефіцієнта кореляції Пірсона.
ПРИКЛАД 3.3. Вивчається залежність між продуктивністю праці робітників Х (тис. грн.) та їх емоційним відношенням до своєї професійної діяльності Y (бали). Відповідні дані подано у таблиці 3.8. Оцінити силу зв’язку між досліджуваними факторами за коефіцієнтом кореляції Спірмена. Перевірити його статистичну значущість.
Таблиця 3.8
| Х | |||||||||||||||
| Y |
Розв’язок. Дані таблиці 3.8 є вибірковими парами значень  ,
,  ; п – кількість пар, п=15. Знайдемо коефіцієнт кореляції Спірмена, необхідні розрахунки оформимо у вигляді таблиці (табл. 3.9), використовуючи позначення:
; п – кількість пар, п=15. Знайдемо коефіцієнт кореляції Спірмена, необхідні розрахунки оформимо у вигляді таблиці (табл. 3.9), використовуючи позначення: 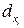 – ранг хі,
– ранг хі,  – ранг уі.
– ранг уі.
Таблиця 3.9
| хі | |||||||||||||||
| yі | |||||||||||||||
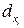
| 4,5 | 8,5 | 4,5 | 8,5 | |||||||||||

| 2,5 | 2,5 | |||||||||||||
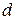 і і
| -1 | -2 | 2,5 | 0,5 | -4 | -4 | 0,5 | 5,5 | |||||||
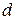 і2 і2
| 6,25 | 0,25 | 0,25 | 30,25 |
Пояснимо, як заповнюється рядок 3: знаходимо найменше зі значень хі (це 26) та присвоюємо йому ранг 1; знаходимо наступне найменше (це 28) і присвоюємо йому ранг 2; наступним найменшим є 31, йому присвоюємо ранг 3; наступними найменшими є два значення 32, якщо б вони були різними, то їм би присвоїли ранги 4 і 5, але оскільки вони однакові, то присвоюємо їм середній ранг  ; і т.д.
; і т.д.
Знаходимо суму квадратів різностей рангів: 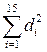 =1+4+1+6,25+ +0,25+16+16+1+0,25+30,25=76.
=1+4+1+6,25+ +0,25+16+16+1+0,25+30,25=76.
Знаходимо поправки, що пов’язані з однаковими рангами. В ряду рангів 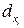 є дві групи однакових рангів, в перший з них 2 елемента, в другій теж два. Отже,
є дві групи однакових рангів, в перший з них 2 елемента, в другій теж два. Отже, 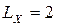 ,
,  .
.
В ряду рангів  є дві групи однакових рангів, в перший з них 2 елемента, в другій три елемента. Отже,
є дві групи однакових рангів, в перший з них 2 елемента, в другій три елемента. Отже, 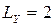 ,
, 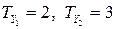 .
.
Підставимо отримані дані в формули (3.6) і знайдемо поправки:
 ;
;
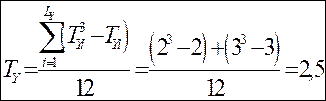 .
.
Знайдемо коефіцієнт кореляції Спірмена за формулою (3.6):
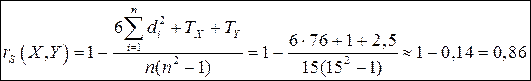 .
.
За значенням коефіцієнта кореляції можна зробити висновок, що між Х та Y існує сильний додатній зв’язок.
Перевіримо статистичну значущість знайденого коефіцієнта кореляції. Розрахуємо t-статистику за формулою (3.4): 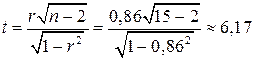 . Знайдемо tкрит, враховуючи, що l=п-2=15-2=13. Оберемо рівень значущості
. Знайдемо tкрит, враховуючи, що l=п-2=15-2=13. Оберемо рівень значущості  =0,001. Тоді tкрит=СТЬЮДРАСПОБР (0,001; 13)=4,22.
=0,001. Тоді tкрит=СТЬЮДРАСПОБР (0,001; 13)=4,22.
Оскільки розраховане значення t-статистики більше критичного 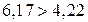 , то коефіцієнт кореляції можна вважати значимим на обраному рівні
, то коефіцієнт кореляції можна вважати значимим на обраному рівні  =0,001.
=0,001.
Висновок. Між продуктивністю праці та емоційним відношенням працівника до професійної діяльності існує сильний додатній зв’язок. Висновок дійсний для всієї генеральної сукупності, з якої було зроблено вибірку.
ПРИКЛАД. Для вивчення залежності урожайності зернових культур Z (ц/га) від якості пашні Х (бали) і кількості внесеного добриву Y (кг/га) було проведено дослідження 6 фермерських хазяйств, результати якого надано у таблиці 3.10. Визначити силу зв’язку між Z та Х та Y, використовуючи множинний коефіцієнт кореляції. Порівняти силу зв’язку між Z та Х і між Z та Y за частинними коефіцієнтами кореляції.
Таблиця 3.10
| Х | ||||||
| Y | 2,1 | 2,3 | 2,4 | 2,6 | 2,9 | |
| Z | 22,1 | 25,3 | 28,5 |
Розв’язок. За умов задачі необхідно для об’єкту, що характеризується трьома ознаками Х, Y та Z (k=3), розрахувати множинний коефіцієнт кореляції 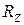 і частинні коефіцієнти кореляції
і частинні коефіцієнти кореляції  та
та 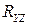 на основі 6 взаємопов’язаних тройок вибіркових даних
на основі 6 взаємопов’язаних тройок вибіркових даних 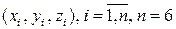 .
.
Побудуємо матрицю парних коефіцієнтів кореляції, які обчислимо за формулою (3.3). Розрахунки для зручності оформимо у вигляді таблиці (табл. 3.11).
Таблиця 3.11
| Розрахункова таблиця | Суми | ||||||
| хі | |||||||
| yі | 2,1 | 2,3 | 2,4 | 2,6 | 2,9 | 15,3 | |
| zі | 22,1 | 25,3 | 28,5 | 142,9 | |||

| |||||||

| 4,41 | 5,29 | 5,76 | 6,76 | 8,41 | 39,63 | |

| 488,41 | 640,09 | 812,25 | 3489,75 | |||
| хі yі | 54,6 | 80,5 | 86,4 | 118,9 | 579,4 | ||
| хі zі | 795,6 | 1282,5 | 5441,1 | ||||
| yі zі | 37,8 | 48,3 | 53,04 | 65,78 | 81,2 | 85,5 |
Отже, за формулою (3.3) маємо:
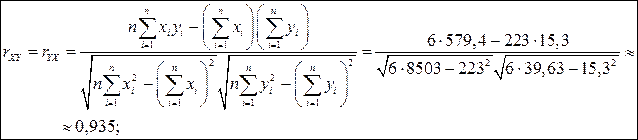
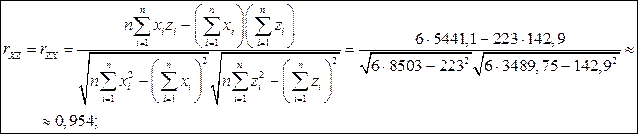
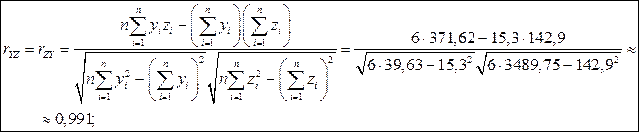
| <== попередня сторінка | | | наступна сторінка ==> |
| Властивості коефіцієнта кореляції Пірсона | | | ГЛІКОГЕННА ФУНКЦІЯ ПЕЧІНКИ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |