
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Властивості збіжних рядів
Відзначимо основні властивості рядів.
1) Якщо збігається ряд, одержаний з даного ряду відкиданням декількох його членів, то збігається і сам даний ряд. І навпаки: якщо збігається даний ряд, то збігається і ряд, одержаний з даного відкиданням декількох членів.
Дійсно, якщо 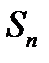 – сума
– сума 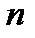 перших членів ряду (1),
перших членів ряду (1), 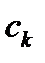 – сума
– сума 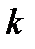 відкинутих членів,
відкинутих членів,  – сума членів ряду, що входять в суму
– сума членів ряду, що входять в суму 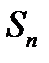 і не входять в
і не входять в 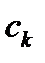 , то
, то 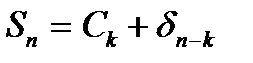 . Якщо існує
. Якщо існує 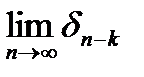 , то існує і
, то існує і 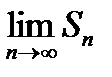 , і навпаки. Таким чином, на збіжність ряду не впливає відкидання скінченого числа його членів.
, і навпаки. Таким чином, на збіжність ряду не впливає відкидання скінченого числа його членів.
2) Якщо ряд (1) збігається і його сума дорівнює 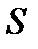 , то ряд
, то ряд
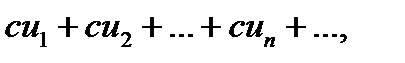 (2)
(2)
де  – яке-небудь фіксоване число, також збігається і його сума дорівнює
– яке-небудь фіксоване число, також збігається і його сума дорівнює 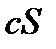 .
.
Дійсно, якщо 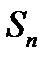 –
– 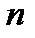 – на частинна сума ряду (1), а
– на частинна сума ряду (1), а 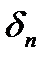 –
– 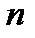 – на частинна сума ряду (2), то
– на частинна сума ряду (2), то 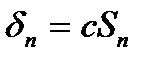 , і
, і 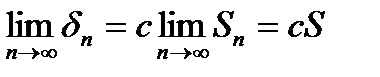 .
.
3) Якщо ряди (1) і
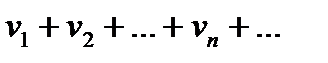 (3)
(3)
збігаються і їх суми, відповідно, дорівнюють 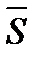 і
і  , то ряди
, то ряди
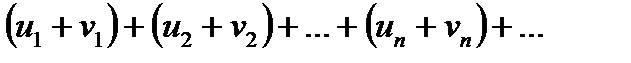 (4)
(4)
та
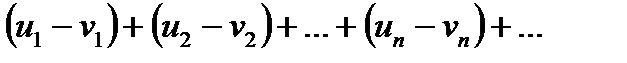 (5)
(5)
також збігаються і їх суми, відповідно, дорівнюють 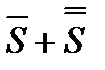 та
та 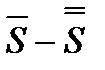 .
.
Дійсно, 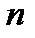 – на частинна сума ряду (4)
– на частинна сума ряду (4) 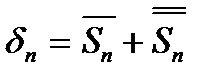 , де
, де 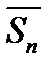 та
та 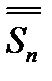 –
– 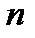 – ні частинні суми рядів (1) і (3). Маємо:
– ні частинні суми рядів (1) і (3). Маємо:
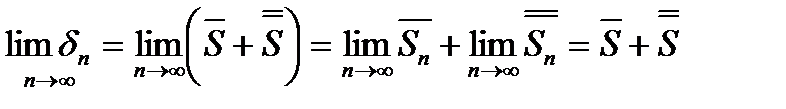 .
.
Аналогічно доводиться, що ряд (5) збігається і його сума дорівнює 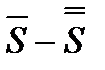 .
.
3. Необхідна ознака збіжності ряду та достатні ознаки збіжності рядів з додатними членами
а) Сформулюємо необхідну ознаку збіжності ряду.
Якщо ряд (1) збігається, то його 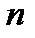 – ний член прямує до нуля при необмеженому зростанні
– ний член прямує до нуля при необмеженому зростанні 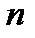 .
.
Дійсно, якщо ряд (1) збігається, то 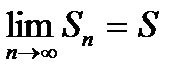 та
та 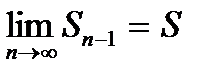 . Таким чином,
. Таким чином, 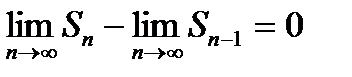 , або
, або 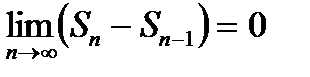 .
.
Це означає, що 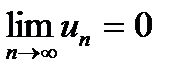 , що і потрібно було довести.
, що і потрібно було довести.
Звідси як наслідок випливає достатна ознака розбіжності ряду: якщо 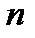 – ний член ряду не прямує до нуля при
– ний член ряду не прямує до нуля при 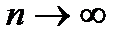 , то ряд розбігається.
, то ряд розбігається.
Приклад №3. Дослідити на збіжність ряд 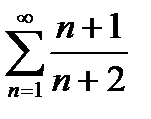 .
.
Розв'яування. Оскільки 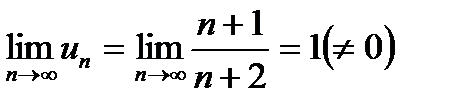 , то ряд збігається.
, то ряд збігається.
Зауважимо, що у випадку, коли 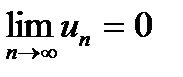 , ряд може бути як збіжним, так і розбіжним.
, ряд може бути як збіжним, так і розбіжним.
Так, наприклад, далі буде показано, що так званий гармонічний ряд

розбігається, хоча 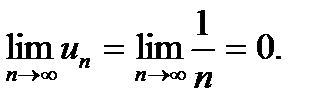
б) Розглянемо ряди (1) і (3) з додатними членами:
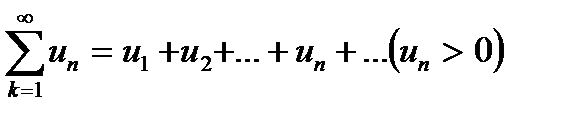
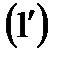
та
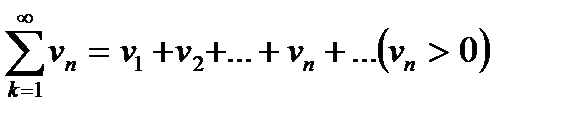
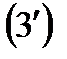
Нехай кожен член ряду 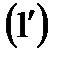 не більше відповідного члена ряду
не більше відповідного члена ряду 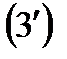 , тобто
, тобто 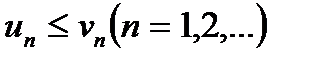 . Тоді:
. Тоді:
1) якщо збігається ряд 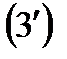 , то збігається і ряд
, то збігається і ряд 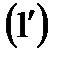 .
.
2) якщо розбігається ряд 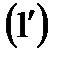 , то розбігається і ряд
, то розбігається і ряд 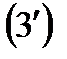 .
.
Це – так звана ознака порівняння.
Дійсно, якщо ряд 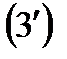 збігається, то його
збігається, то його 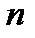 -на частинна сума не перевищує
-на частинна сума не перевищує 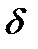 , де
, де 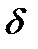 – сума ряду
– сума ряду 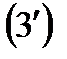 . Але
. Але 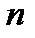 -на частинна сума
-на частинна сума 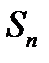 ряду
ряду 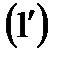 не перевищує
не перевищує 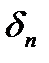 і, отже, обмежена зверху числом
і, отже, обмежена зверху числом 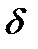 . А це означає, що ряд
. А це означає, що ряд 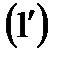 збігається.
збігається.
Якщо ж ряд 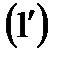 розбігається, то його частинні суми необмежено зростають:
розбігається, то його частинні суми необмежено зростають: 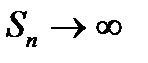 . Оскільки
. Оскільки 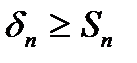 , то і
, то і 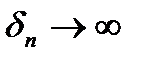 . Оскільки
. Оскільки 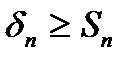 , то і
, то і 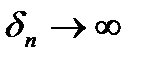 . Значить, ряд
. Значить, ряд 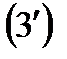 розбігається, що і потрібно було довести.
розбігається, що і потрібно було довести.
Приклад №4. Дослідити на збіжність ряди.
а) 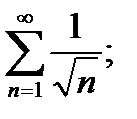 б)
б) 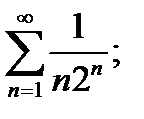 за допомогою ознаки порівняння.
за допомогою ознаки порівняння.
Розв'язування.
а) Оскільки 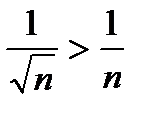 , а ряд
, а ряд 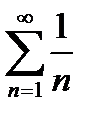 розбігається, то і ряд
розбігається, то і ряд 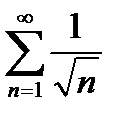 також розбігається.
також розбігається.
б) Оскільки 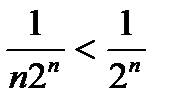 , а ряд
, а ряд 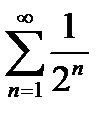 збігається як геометрична прогресія, знаменник якої менший від одиниці, то і ряд
збігається як геометрична прогресія, знаменник якої менший від одиниці, то і ряд 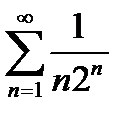 збігається.
збігається.
На практиці часто користуються граничною ознакою порівняння рядів з додатними членами: якщо границя відношення 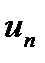 та
та 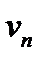 існує і не дорівнює нулю
існує і не дорівнює нулю
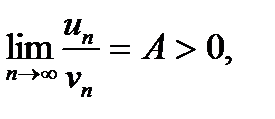
то ряди 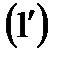 і
і 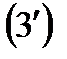 або обидва збігаються, або обидва розбігаються.
або обидва збігаються, або обидва розбігаються.
в) Розглянемо достатні ознаки збіжності ряду, які використовують лише вирази для його членів.
Ознака Даламбера. Нехай дано ряд 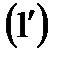 з достатними членами. Якщо при
з достатними членами. Якщо при 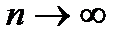 існує границя відношення наступного члена до попереднього
існує границя відношення наступного члена до попереднього 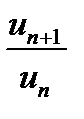 , що дорівнює
, що дорівнює 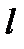 :
:
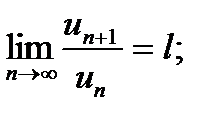
то при 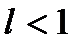 , ряд збігається, а при
, ряд збігається, а при 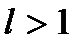 – розбігається (при
– розбігається (при 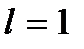 ряд може бути як збіжним, так і розбіжним).
ряд може бути як збіжним, так і розбіжним).
Приклад №5. Дослідити на збіжність ряд 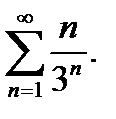
Розв'язування. Тут 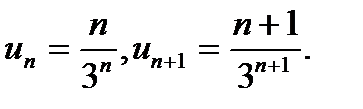
Тому 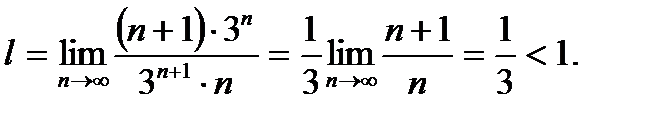
Отже, даний ряд збігається.
Зауважимо, що коли 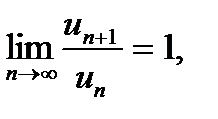 але
але 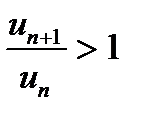 для всіх номерів
для всіх номерів  , починаючи з деякого, то ряд розбігається, оскільки
, починаючи з деякого, то ряд розбігається, оскільки 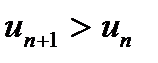 і загальний член не прямує до нуля при
і загальний член не прямує до нуля при 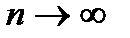 . Ряд буде розбіжним і в тому випадку, коли
. Ряд буде розбіжним і в тому випадку, коли 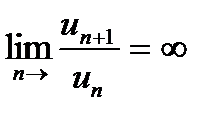 .
.
Ознака Коші. Якщо для ряду 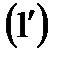 з додатними членами величина
з додатними членами величина 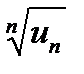 має скінченну границю
має скінченну границю 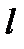 при
при 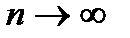 , тобто
, тобто
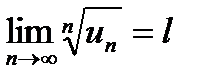 ,
,
то при 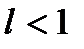 ряд збігається, при
ряд збігається, при 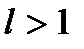 – розбігається (при
– розбігається (при 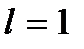 ряд може бути як збіжним, так і розбіжним).
ряд може бути як збіжним, так і розбіжним).
Приклад №6. Дослідити на збіжність ряд 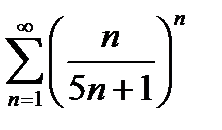 .
.
Розв'язок. Застосуємо ознаку Коші:
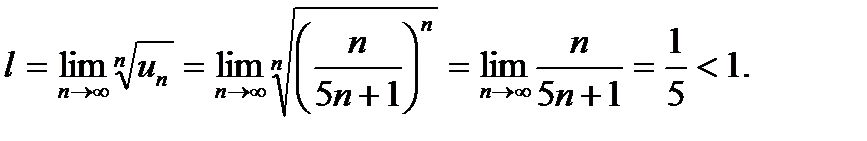
Ряд збігається.
Інтегральна ознака збіжності ряду.
Нехай члени ряду 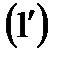 додатні та не зростають, тобто
додатні та не зростають, тобто 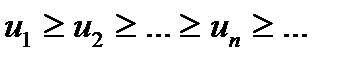 і нехай
і нехай  – така неперервна незростаюча функція, що
– така неперервна незростаюча функція, що 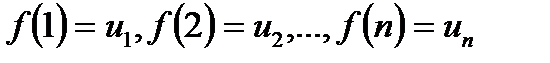 . Тоді справедливі наступні твердження: якщо невласний інтеграл
. Тоді справедливі наступні твердження: якщо невласний інтеграл 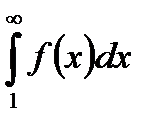 збігається, то збігається і ряд
збігається, то збігається і ряд 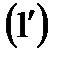 ; якщо вказаний інтеграл розбігається, то розбігається і ряд
; якщо вказаний інтеграл розбігається, то розбігається і ряд 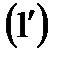 .
.
Приклад №7. Дослідити на збіжність ряд 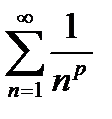 .
.
Розв'язування. Покладемо 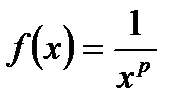 та застосуємо інтегральну ознаку. маємо:
та застосуємо інтегральну ознаку. маємо: 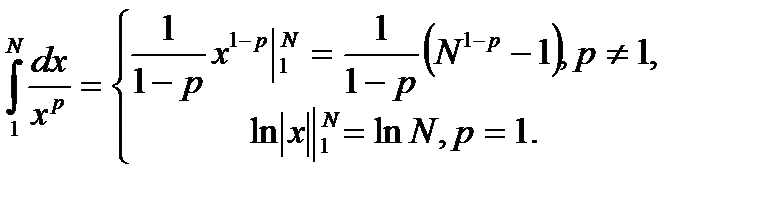 .
.
Отже, при 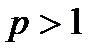 буде
буде 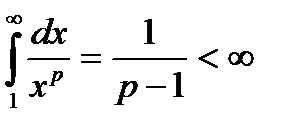 – ряд збігається. У випадку
– ряд збігається. У випадку 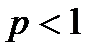
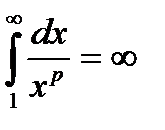 – ряд розбігається. І, нарешті, при
– ряд розбігається. І, нарешті, при 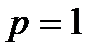 (випадок гармонічного ряду)
(випадок гармонічного ряду) 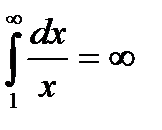 – ряд розбігається.
– ряд розбігається.
4. Знакозмінні ряди
Вивчимо питання про ряди з довільними членами.
а) Розглянемо ряд, знаки якого строго чергуються:
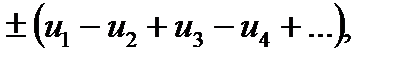 (6)
(6)
де 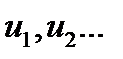 – додатні числа. Має місце
– додатні числа. Має місце
Теорема Лейбніца. Якщо в ряді (6) абсолютні значення членів ряду спадають, тобто
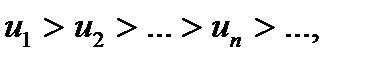
і загальний член ряду прямує до нуля, то ряд збігається, причому його сума за абсолютною величиною менша від 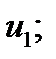 залишок ряду
залишок ряду 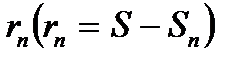 за абсолютною величиною менший за абсолютну величину першого з відкинутих членів:
за абсолютною величиною менший за абсолютну величину першого з відкинутих членів: 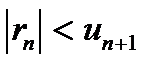 .
.
Приклад №8. Дослідити на збіжність ряд
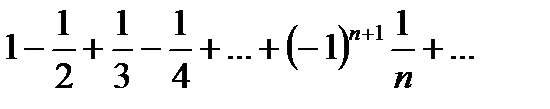
Розв'язок. Цей ряд збігається, оскільки 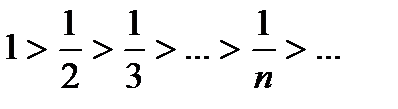 та
та 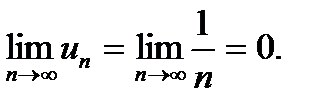 При цьому частинна сума
При цьому частинна сума 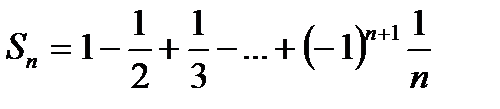 відрізняється від суми
відрізняється від суми 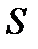 ряду на величину меншу, ніж
ряду на величину меншу, ніж 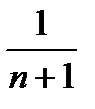 .
.
б) Для рядів з довільними знаками їх членів найчастіше користуються наступною достатньою ознакою збіжності.
Якщо ряд, складений із абсолютних величин членів даного ряду, збігається, то збігається і даний ряд.
Обернене твердження, взагалі кажучи, невірне. Так, наприклад, ряд
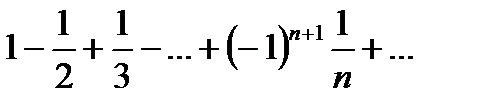
збігається згідно з теоремою Лейбніца, а ряд, складений із абсолютних величин його членів (гармонічний ряд)
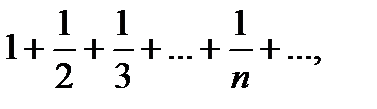
розбігається (наприклад, згідно з інтегральною ознакою).
Ряд, абсолютні величини членів якого утворюють збіжний ряд, називається абсолютно збіжним. Якщо ряд збігається, а ряд, утворений з абсолютних величин його членів, розбігається, то даний ряд називається неабсолютно або умовно збіжним.
Розглянутий вище ряд є умовно збіжним.
Виявляється, що коли ряд збігається абсолютно, то він залишається абсолютно збіжним при будь-якій перестановці його членів. При цьому сума ряду не залежить від порядку його членів. Якщо ж ряд збігається умовно, то яким би не було число А, можна так переставити члени цього ряду, щоб його сума виявилась рівною А. Більше того, можна, так переставити члени умовно збіжного ряду, що ряд, одержаний після перестановки, виявиться розбіжним.
| <== попередня сторінка | | | наступна сторінка ==> |
| Поняття про ряд та його суму. | | | Семінарське заняття 13 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |