
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Математичне сподівання дискретної випадкової величини, його зміст та властивості
Якщо закон розподілу дискретної випадкової величини невідомий, користуються числовими характеристиками випадкової величини, які описують цю величину сумарно - математичним сподіванням, дисперсією, середнім квадратичним відхиленням.
Математичним сподіванням дискретної випадкової величини називається сума добутків всіх її можливих значень на їх ймовірності:
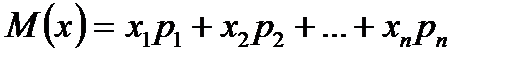 .
.
Таким чином, математичне сподівання дискретної випадкової величини – величина стала.
Якщо, наприклад,  – число появ події в одному випробуванні, то закон розподілу має вигляд
– число появ події в одному випробуванні, то закон розподілу має вигляд

| ||
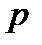
| 
| 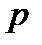
|
При цьому 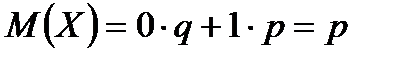 .
.
Термін “математичне сподівання” пов’язаний з азартними іграми. Якщо гравець 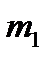 раз вигравав суму
раз вигравав суму 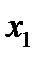 ,
, 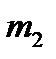 раз –
раз – 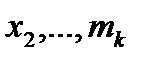 раз –
раз – 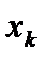 , то середня величина
, то середня величина 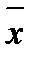 виграшу в одній з
виграшу в одній з 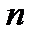 партій (
партій ( 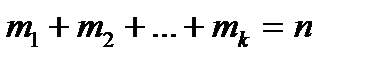 ) визначається так:
) визначається так:
 ,
,
де 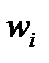 – відносна частота значення
– відносна частота значення 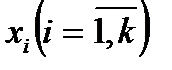 . При
. При 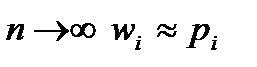 . Таким чином,
. Таким чином,
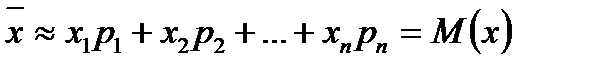 .
.
Отже, математичне сподівання наближено дорівнює (тим точніше, чим більше 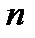 ) середньому арифметичному значень випадкової величини. З точки зору азартного гравця математичне сподівання виграшу – це середнє значення очікуваного виграшу.
) середньому арифметичному значень випадкової величини. З точки зору азартного гравця математичне сподівання виграшу – це середнє значення очікуваного виграшу.
Користуючись означенням математичного сподівання, можна довести його основні властивості.
1) Математичне сподівання сталої величини дорівнює самій сталій: 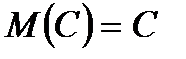 .
.
2) Постійний множник можна виносити за знак математичного сподівання: 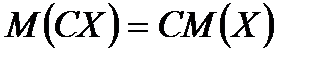 .
.
3) Математичне сподівання добутку двох незалежних випадкових величин дорівнює добутку їх математичних сподівань.
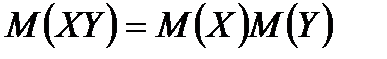 .
.
Аналогічна властивість має місце щодо добутку кількох взаємно незалежних випадкових величин.
4) Математичне сподівання суми двох випадкових величин (як незалежних, так і залежних) дорівнює сумі математичних сподівань доданків: 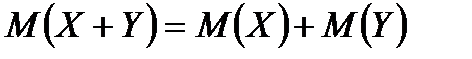 .
.
Аналогічна властивість має місце для суми кількох випадкових величин.
Приклад №5. Нехай проводиться 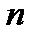 незалежних випробувань, у кожному з яких ймовірність появи події А постійна і дорівнює
незалежних випробувань, у кожному з яких ймовірність появи події А постійна і дорівнює 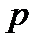 . Визначимо середнє число появ події А у цих випробуваннях.
. Визначимо середнє число появ події А у цих випробуваннях.
Нехай 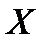 – число появ події А в
– число появ події А в 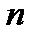 випробуваннях;
випробуваннях; 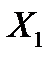 – число появ події А в 1-му випробуванні;
– число появ події А в 1-му випробуванні; 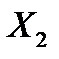 – в другому, ...,
– в другому, ..., 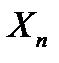 – в
– в 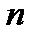 -ому випробуванні. Загальне число появ події А визначається рівністю
-ому випробуванні. Загальне число появ події А визначається рівністю
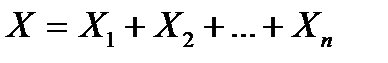 .
.
Отже, 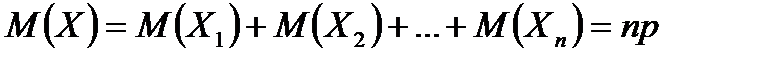 .
.
Таким чином, математичне сподівання 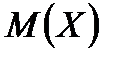 числа появ події А в
числа появ події А в 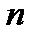 незалежних випробуваннях дорівнює добуткові числа випробувань на ймовірність появи події в кожному випробуванні:
незалежних випробуваннях дорівнює добуткові числа випробувань на ймовірність появи події в кожному випробуванні: 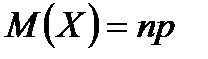 .
.
Приклад №6. Двоє робітників різної кваліфікації працюють на однакових машинах. Числа 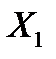 та
та 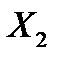 бракованих виробів за деякий інтервал часу у кожного робітника є незалежними випадковими величинами з такими законами розподілу:
бракованих виробів за деякий інтервал часу у кожного робітника є незалежними випадковими величинами з такими законами розподілу:
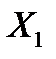
| |||
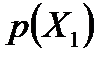
| 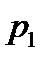
| 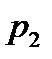
| 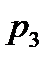
|
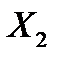
| |||
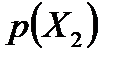
| 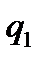
| 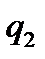
| 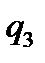
|
Скласти закон розподілу для загального числа бракованих виробів 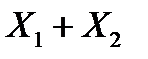 та середнього їх числа
та середнього їх числа 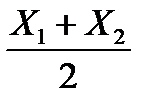 , а також визначити відповідні математичні сподівання.
, а також визначити відповідні математичні сподівання.
Щоб розв’язати сформульовану задачу, складемо закон розподілу для загальної кількості бракованих виробів:
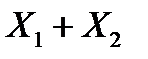
| |||||
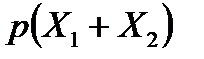
| 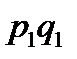
| 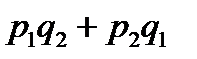
| 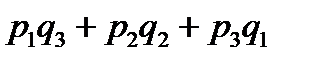
| 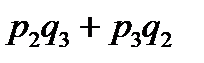
| 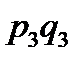
|
Закон розподілу середнього числа 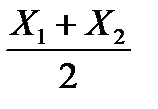 бракованих виробів:
бракованих виробів:
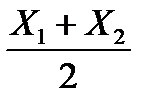
| 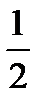
| 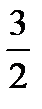
| |||
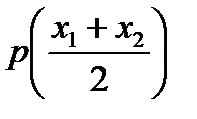
| 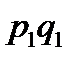
| 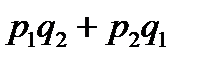
| 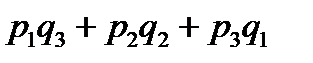
| 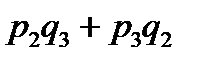
| 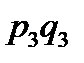
|
Математичні сподівання 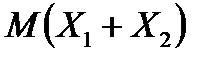 і
і 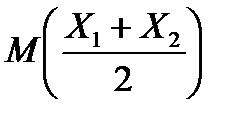 можна знайти, користуючись означенням математичного сподівання.
можна знайти, користуючись означенням математичного сподівання.
Ми розв’яжемо цю задачу, користуючись властивостями математичного сподівання:
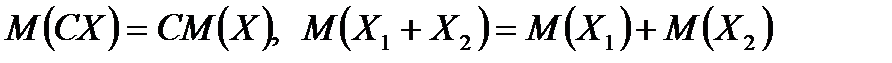 .
.
Маємо:
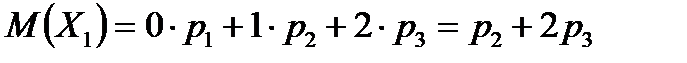 ;
;
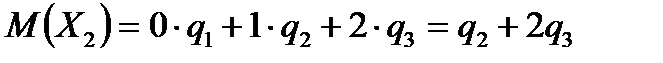 .
.
Отже,
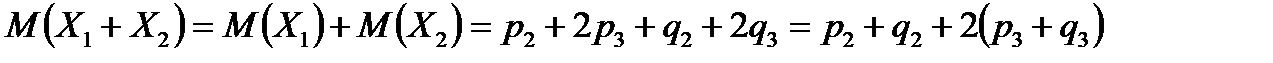 ;
;
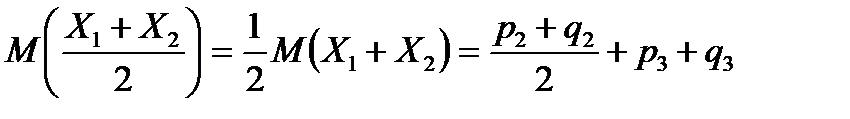 .
.
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклади дискретних випадкових величин та їх законів розподілу | | | Дисперсія дискретної випадкової величини, її властивості |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |