• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Регресійний аналіз і кореляція. Основні означення

Нехай ми маємо дві випадкові величини – і . Кожну з них окремо можна характеризувати, наприклад, за допомогою її середнього значення, дисперсії тощо. Вивчаючи та в сукупності, будемо розглядати ще і вплив однієї величини на іншу. При цьому величина може бути і не випадковою, а заданою експерементатором. Можливі такі ситуації.

1. та – незалежні величини: зміна не впливає на розподіл .

2. та пов’язані функціональною залежністю: кожному значенню 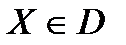відповідає цілком певне значення (тут 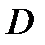– область визначення функції).

3. Між існує статистична (стохастична) залежність, коли одному і тому ж значенню величини відповідає статистична сукупність значень величини з законом розподілу, що змінюється зі зміною . Якщо, зокрема, при зміні однієї величини ( ) змінюється середнє значення другої ( ), то статистична залежність називається кореляційною. Отже, кореляційна залежність – це функціональна залежність між значеннями величини та умовними середніми значеннями випадкової величини (тобто середніми значеннями величини , обчисленими при даних ).

Неповною називається кореляція, коли одній величині (наприклад, ) надаються певні фіксовані значення 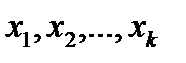і для кожного з них шляхом експерименту знаходять сукупність значень у величини .

Повною називається кореляція, коли кожен із відібраних елементів статистичної сукупності об’єктів вивчається відразу і по , і по .

В теорії кореляції розв’язується такі дві основні задачі:

1) питання про форму кореляційного зв’язку між та (підбір певного виду функціональної залежності);

2) оцінка тісноти кореляційного зв’язку між та (наскільки близька залежність до вибраної функціональної).

Перша з цих задач розв’язується за допомогою регресій. Емпірична лінія регресії – це ламана лінія, яка з’єднує точки з координатами 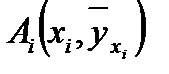(тут 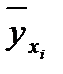– умовна середня 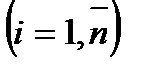). Теоретичною лінією регресії по називається лінія, яка “згладжує” емпіричну лінію регресії. Її рівняння, таким чином, дає наближений аналітичний вираз регресії. Щоб одержати теоретичну лінію регресії, спочатку підбирають тип лінії, навколо якої групуються експериментальні точки: пряма, гіпербола, показникова функція і т.д. Далі обчислюють параметри вибраної залежності (наприклад, методом найменших квадратів).

Кореляційна залежність між випадковими величинами та називається лінійною кореляцією, якщо обидва теоретичні рівняння регресії 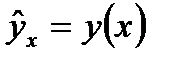та 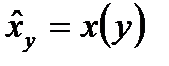лінійні (тобто їх графіки – прямі лінії). В противному випадку кореляційна залежність називається нелінійною.

Якщо – не випадкова величина, то кореляційна залежність між та називається лінійною, якщо теоретичне рівняння 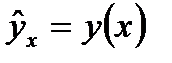лінійне, і нелінійною – в противному випадку.

2. Знаходження параметрів теоретичного рівняння регресії 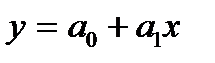методом найменших квадратів

Розглянемо питання про знаходження параметрів теоретичного рівняння регресії 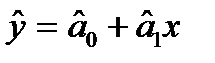методом найменших квадратів.

Нехай дано 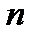точок 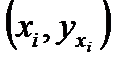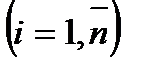(для простоти позначимо 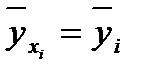). Знайдемо 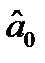та 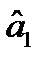методом найменших квадратів. Для цього будемо вимагати, щоб сума квадратів відхилень точок від лінії 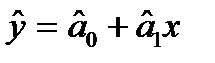вздовж осі була найменшою (рис.1).

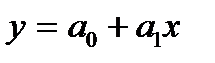
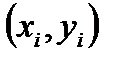
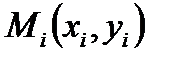
0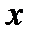

Рис. 1. Метод найменших квадратів.

Маємо: 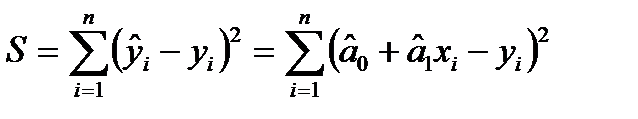. Оскільки – функція, залежна від двох змінних і , для знаходження її мінімуму шукаємо частинні похідні 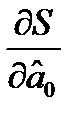та :

,

.

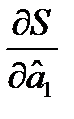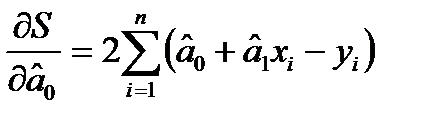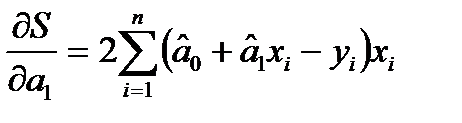Прирівнюючи ці похідні до нуля, одержимо так звану нормальну систему відносно 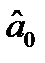і :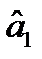

.

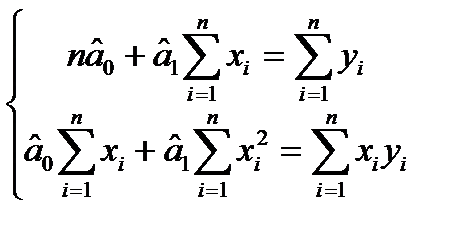Звідси маємо:

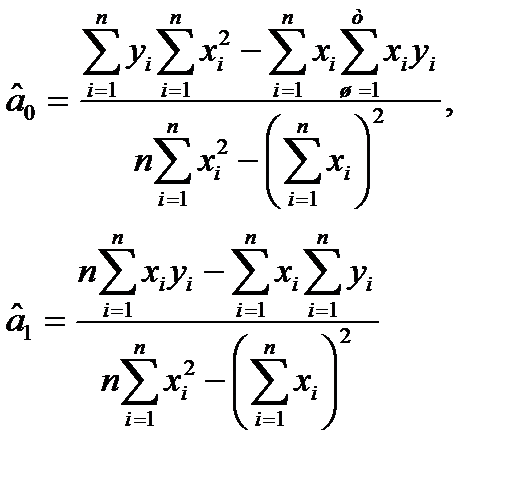
Параметри 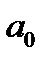і 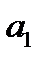теоретичного рівняння регресії 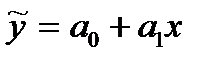можна оцінити за формулами (для рівняння значущості )

,

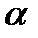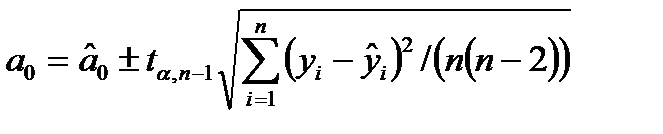
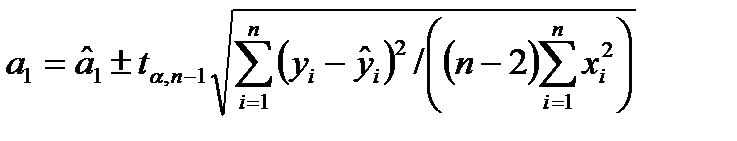де 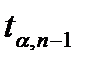– статистика Стьюдента при рівні значущості 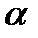; 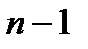– кількість степенів свободи (критична область двохстороння).

Зауваження. Коефіцієнт 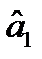можна представити у вигляді

,

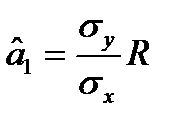де 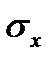та 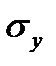– вибіркові середні квадратичні відхилення, а 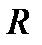– вибірковий коефіцієнт кореляції:

.

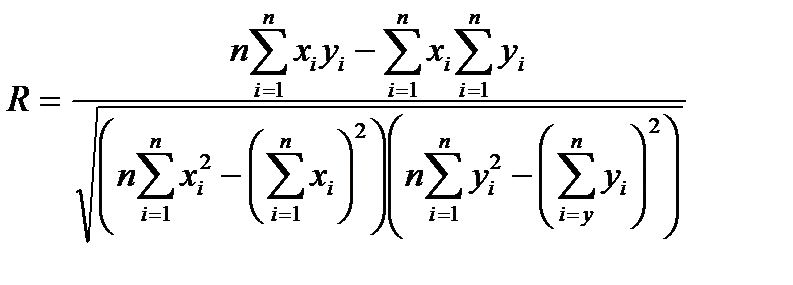Цей коефіцієнт є статистичною оцінкою невідомого теоретичного коефіцієнта кореляції 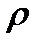, який визначається рівністю:

.

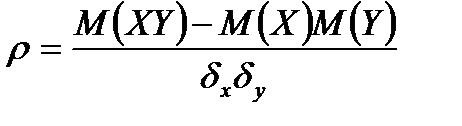Аналогічно можна знайти вибіркове рівняння прямої лінії регресії 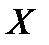на :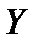

,

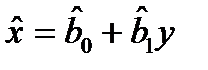Цікаво визначити, що у швейному і взуттєвому виробництвах при виборі ознак, за якими стандартизують одяг і взуття, велику роль відіграє оцінка близькості кореляційної залежності між і і лінійної функціональної залежності. Це пов’язане з тим, що розміри людського тіла (наприклад, зріст, повнота, довжина, ширина кисті руки) відповідають нормальним законам розподілу, а в таких випадках кореляційні залежності близькі до лінійних функцій.

Переглядів: 569