• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Правило перевірки нульової гіпотези

Вибірковий коефіцієнт кореляції 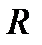, як і будь-яка статистична оцінка, є наближеною характеристикою теоретичного коефіцієнта кореляції . У тих випадках, коли коефіцієнт 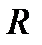малий, важливо встановити, значущий він чи ні. Якщо вибірковий коефіцієнт кореляції 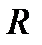значущий, то і корельовано.

В противному випадку між та немає лінійної залежності. Отже, при певному рівні значущості 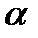(наприклад, 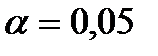) слід перевірити нульову гіпотезу 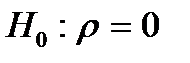про рівність нулю генерального коефіцієнта кореляції при конкуруючій гіпотезі .

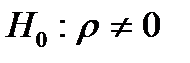Критерій перевірки нульової гіпотези – випадкова величина 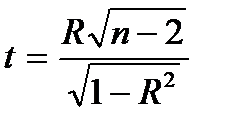, яка має розподіл Стьюдента з 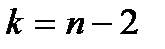степенями свободи при справедливості нульової гіпотези.

Сформулюємо правило перевірки нульової гіпотези.

1) Обчислити .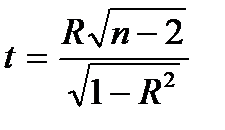

2) По таблиці критичних точок розподілу Стьюдента за даними 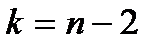та 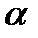знайти .

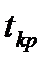3) Якщо 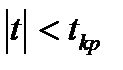., то немає підстав відкинути нульову гіпотезу. У цьому випадку коефіцієнт 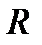незначущий, а випадкові величини і некорельовані (лінійно незалежні).

Якщо 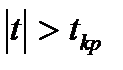, то нульову гіпотезу відкидають. Коефіцієнт 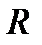значущий. Випадкові величини і корельовані.

Наприклад. Сировина, яка надходить на завод, містить дві корисні речовини – мінерали А та В. Проведені аналізи показали, що в партіях з підвищеним вмістом мінералу А виявлено більш високий вміст мінералу В. Аналізи 10 зразків сировини наведені в таблиці. Знайти коефіцієнт кореляції, оцінити тісноту зв’язку між вмістом мінералів А і В у сировині. Скласти рівняння прямої лінії регресії 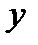на .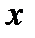

(%)
(%)

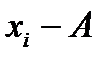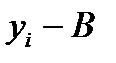Обчислюємо коефіцієнт кореляції: 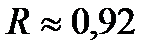. Знаходимо 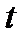: 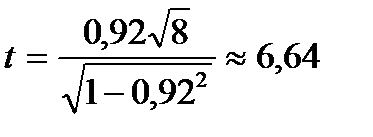. За таблицею критичних точок розподілу Стьюдента для 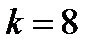та 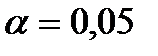знаходимо: 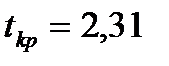. В розглядуваному прикладі 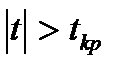. Отже, коефіцієнт 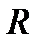значущий. Величини А та В корельовані.

Обчисливши параметри 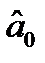і 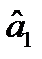, одержимо рівняння регресії:

.

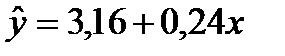Зауважимо, що кореляційно-регресійний аналіз є математичним апаратом багатьох задач прогнозування. За допомогою регресії можна розв’язати задачу прогнозування величини 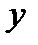для даного фактора 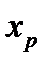. Середнє значення прогнозу знаходимо за формулою 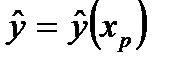, де 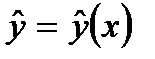– рівняння теоретичної лінії регресії. У випадку лінійного рівняння .

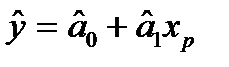Дисперсія прогнозу середніх значень

,

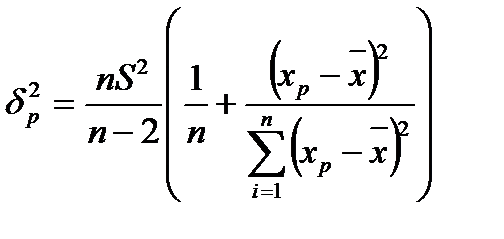де 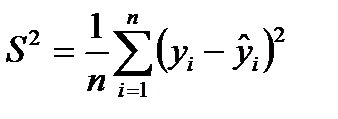. похибка прогнозу 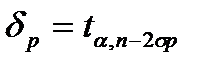, де 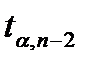– статистика. Стьюдента при рівні значимості 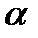. Для прогнозу величини 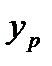з надійністю 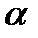можна вказати довірчий інтервал

.

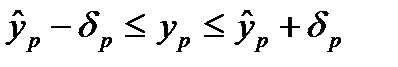Похибка прогнозу виникає із-за впливу врахованих факторів (нагадуємо, що рівняння регресії має ймовірний характер) і через невідповідність вибіркової сукупності, за якою будувалося рівняння регресії, генеральній сукупності.

Якщо 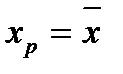, то границі довірчого інтервалу розміщені найближче одна до одної.

Переглядів: 617