Проблеми реалізації алгоритму

При виконанні проектувальних розрахунків вручну трудомісткими є кількаразові звертання до таблиць (11) з виконанням інтерполяції. Безпосереднє програмування даного завдання для ЕОМ призводить до необхідності введення значних масивів початкових даних. Для складання компактних програм і при розрахунках вручну зручно апроксимувати таблиці (11) простими формулами з невеликим числом варійованих параметрів.

1.5 Апроксимація таблиць φ = φ (λ)

Типова форма графіка залежності φ від λ зображена на малюнку 1.

Малюнок 1. Графік φ = φ (λ)

Таблиці значень коефіцієнтів φ для різних матеріалів наводяться у довідниках і підручниках [1,3,5-10]. Звичайно таблиці будуються для інтервалу 0 < λ <200.

Апроксимація поліномом. Із зовнішнього вигляду кривої φ = φ (λ) випливає, що необхідний поліном ступеня не нижче 3-ого

φ (λ)=a₀ + a₁ λ +a₂ λ² + a₃ λ³ (14)

На перший погляд здається, що необхідно використовувати формулу φ (λ)=1 + a₁ λ +a₂ λ² + a₃ λ³, яка автоматично прив'язала б функцію φ (λ) до точки (0,1). Однак вираз (14) має додатковий ступінь свободи, що дозволяє зменшити середні похибки апроксимації.

Результати визначення коефіцієнтів a_i методом найменших квадратів (МНК) наведено у таблиці 1. Слід зазначити, що обчислення по формулі (14) приводять до малих різниць близьких величин. Тому слід уникати округлення коефіцієнтів a_i і використовувати всі значущі цифри, наведені в таблиці 1.

Апроксимація експонентою. Для більш точного представлення кривої φ (λ) в інтервалі 0< λ< 200 можна було б скористатися рівнянням

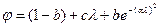(15a)

що містить три параметри. Однак, як показали розрахунки, з достатньою для практики точністю графік функції φ = φ (λ) може бути представлений для цього інтервалу залежністю

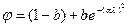(15б)

Параметри b і a можуть бути підібрані як МНК, так і іншими методами наближеного аналізу з яких найбільш простий у реалізації метод колокацій (МК) використання якого у нашому випадку полягає у наступному.

Припустимо, відомі коефіцієнти φ₁ і φ₂ для двох значень гнучкості λ₁ і λ₂. Підставивши у формулу (15б) відповідні φ і λ, отримаємо два рівняння із двома невідомими a і b. Очевидно, що крива, задовольняюча рівнянню (15б), при цьому буде проходити через три точки з координатами (0,1), (λ₁, φ₁), (λ₂, φ₂) (точки колокацій (ТК), малюнок 1). У цьому випадку параметр b може бути знайдений з рішення трансцендентного рівняння

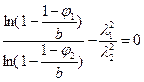(16)

і параметр a - по формулі

,…і=1,2 (17)

Недоліком МК є невизначеність вибору точок колокацій, від яких залежить точність апроксимації, особливо при малому числі ТК (у розглянутому окремому випадку приймалися λ₁ = 0.5λ₂).

У таблиці 2 дані значення параметрів a і b, знайдені за описаною схемою для різних матеріалів. При цьому для вирішення рівняння (16) використовувалися дані з довідників [5, 6, 9] і метод половинного ділення [4].

Таблиця 1. Коефіцієнти a_i у формулі (14)

Матеріал стрижня	Діапазон значень λ	а₀	а₁×10²	а₂×10⁴	а₃×10⁶
1 Сталь класу 38/23 2––“”–– 44/29 3––“”–– 46/33 4––“”–– 52/40 5––“”––– 60/45 6––“”–– 70/60 7––“”–– 85/75 8 Ст 0, 2, 3, 4, 5 9 НЛ-1 10 НЛ-2 (15ХСНД) СПК	0…220 0…220 0…220 0…220 0…220 0…220 0…220 0…200 0…200 0…200 0…200 0…100	1,004318 1,016494 1,021961 1,030598 1,054729 1,073369 0.987300 0,987628 1,008762 0,995307 1,003143	-0,068536 -0,169260 -0,214025 -0.292394 -0,532364 -0,715697 0.121936 0,396687 -0,116613 -0,045446 -0,110939	-0,522620 -0,497074 -0,485396 -0,444941 -0,279710 -0,129279 -0.751707 -76,34876 -0,657878 -0,766780 -2,283945	0,173351 0,179785 0,182670 0,178780 0,149480 0,116339 0.248073 0,2718562 0,254104 0,291598 1,559925
Матеріал стрижня	Діапазон значень λ	а₀	а₁×10²	а₂×10⁴	а₃×10⁶
11 СЧ 12-28; СЧ 15-18; СЧ 15-30; СЧ 15-32; СЧ 15-36;
СЧ 18-36; СЧ 21-40. 12 СЧ 21-44; СЧ 24-44; СЧ 28-48. 13 Амг	0…100 0…150	1,009925 1,006378	-0,391263 -0,114311	-2,327691 -0,871068	1,849383 0,423050
14 Амг6 15 АВТ1 16 Д16Т 17 Кам'яні та армокам'яні елементи 18 Залізобетон 19 Бетон важкий 20 Бетон легкий 21 Дерево (сосна, ялина)	0…150 0…150 0…150 0…150 0…100 0…100 0…100 0…200	1,036413 1,044095 1,071236 1,014077 0,970768 1,008460 1,008787 1,048227	-0,521529 -0,392641 -0,777400 -0,226183 +0,714628 -0,083384 +0,026714 -0,370861	-0,659902 -0,929945 -0,587496 -0,607519 -2,097372 -1,088066 -2,292274 -0,570146	0,417745 0,528714 0,455554 0,294597 0,911068 ,619705 1,767735 0,264138

Таблиця 2. Коефіцієнти a і b апроксимуючої функції (15б)

Матеріал стрижня	Діапазон значень λ	a×10²	b	Максимальна похибка, %
1 Сталь класу 38/23 2 ––“”–– 44/29 3 ––“”–– 46/33 4 ––“”–– 52/40 5 ––“”–– 60/45 6 СЧ 15-30; СЧ 41-40 7 СЧ 21-44; СЧ 28-48 8 Дерево 9 Бетон важкий 10 Бетон легкий	0…200 0…200 0…200 0…200 0…200 0…100 0…100 0…180 0…100 0…80	0,80174 0,88875 0,9254 0,96009 1,020 1,5985 2,0116 1,1877 1,3498 1,9511	0,89238 0,89758 0,90031 0,90676 0,90934 0,91078 0,89566 0,90949 0,65605 0,59180	+ 3 + 3 + 3 +6/-3 +7/-3 + 3 + 5 + 6 + 4 + 4

<== попередня сторінка	\|	наступна сторінка ==>
Алгоритм розрахунків на стійкість	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.