Розділ 3.2. Формула повної ймовірності

Теорема: Ймовірність події А , яка може відбутися лише при умові появи однієї з несумісних подій В₁, В₂, … , В_п, які утворюють повну групу, дорівнює сумі добутків ймовірностей кожної з цих подій на відповідну умовну ймовірність події А.

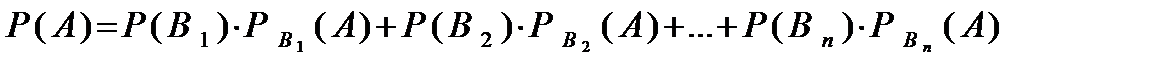. (3.3)

Доведення

Подія А може відбутися, якщо відбудеться одна з несумісних подій В₁, В₂, … , В_п. Тобто поява події А означає здійснення однієї, будь якої з несумісних подій 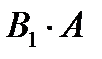, , 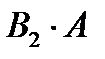… , 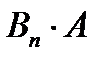Використовуючи теорему додавання (формула 2.1), одержимо

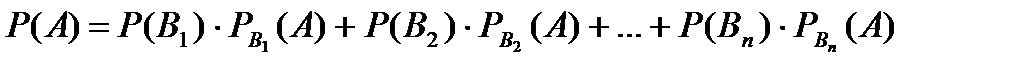Оскільки подія А і події В₁, В₂, … , В_п залежні, тоді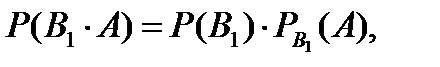

……………………..

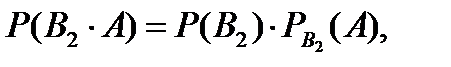
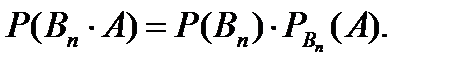
Звідки .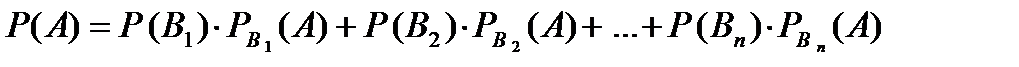

Наприклад:

У першій коробці міститься 15 приладів, з яких 14 якісних, а у другій – 20 приладів, з яких – 17 якісних. Із першої коробки навмання вилучають прилад і перекладають його у другу коробку. Знайти ймовірність того, що прилад, який вилучили з другої коробки, є якісним.

Рішення

Подія А – з другої коробки вилучили якісний прилад.

Тоді мають місце гіпотези (припущення) щодо того, який прилад вилучили з першої коробки:

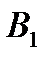- з першої коробки вилучили якісний прилад;

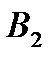- з першої коробки вилучили неякісний прилад.

Тоді: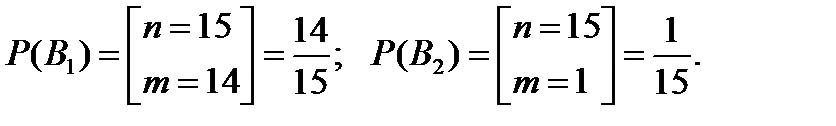

Знайдемо умовні ймовірності того, що з другої коробки вилучили якісний прилад, якщо з першої коробки вилучили якісний прилад 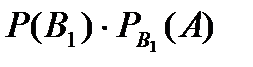та якщо з першої коробки вилучили неякісний прилад :

;

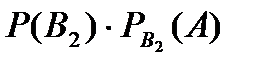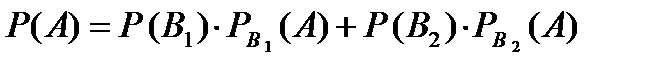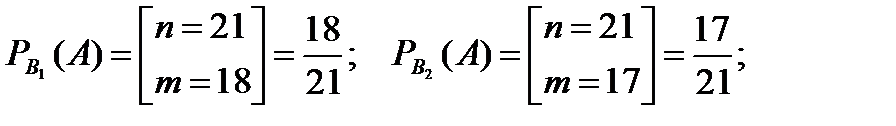
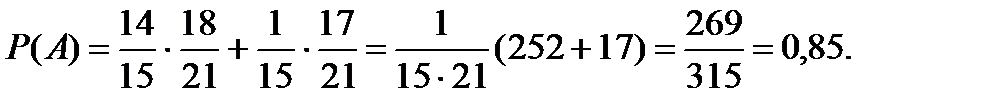
<== попередня сторінка	\|	наступна сторінка ==>
Задачі до розділу 3.1	\|	Задачі до розділу 3.2

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.016 сек.