Розділ 10.3. Завдання до заняття 10

Теоретичні питання до заняття 10

1. Дати означення біноміального закону розподілу дискретної випадкової величини.

2. За якою формулою знаходиться математичне сподівання дискретної випадкової величини, що має біноміальний розподіл? Пояснити її складові.

3. За якою формулою знаходиться дисперсія дискретної випадкової величини, що має біноміальний розподіл? Пояснити її складові.

4. Дати означення розподілу Пуассона.

5. Дати означення геометричного розподілу.

6. Дати означення рівномірного розподілу неперервної випадкової величини.

7. За якою формулою визначається диференціальна функція рівномірного розподілу неперервної випадкової величини.

8. За якою формулою визначається інтегральна функція рівномірного розподілу неперервної випадкової величини.

9. Дати означення нормального розподілу неперервної випадкової величини.

10. Якими параметрами задається нормальний розподіл неперервної випадкової величини.

11. Що є графіком диференціальної функції нормального розподілу неперервної випадкової величини.

12. Як знайти ймовірність попадання в заданий інтервал нормально розподіленої випадкової величини?

Розділ 11.1. Предмет і задачі математичної статистики

Математична статистика займається встановленням закономірностей, яким підкоряються масові випадкові явища, грунтується на використанні методів теорії ймовірностей до статистичних даних – результатів спостережень.

Першою задачею математичної статистики є визначення способів збору і групування статистичних даних, які одержано за результатами спостережень або спеціально поставлених експериментів.

Другою задачею математичної статистики є розробка методів аналізу статистичних даних в залежності від мети дослідження.

Основні терміни:Вибірковою сукупністю або просто вибіркою називають сукупність випадково відібраних об’єктів. Генеральною сукупністю називають сукупність об’єктів, з яких роблять вибірку. Обсягом сукупності називають число об’єктів цієї сукупності.

Наприклад: Якщо із 1000 деталей відібрано для обстеження 100 деталей, тоді обсяг генеральної сукупності 1000 деталей, а вибіркової – 100.

Нехай із генеральної сукупності вилучено вибірку, причому х₁ спостерігалася п₁ раз, х₂ – п₂ раз, ... , х_к- п_к раз і 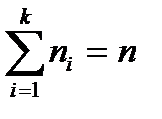- обсяг вибірки. Значення x_i називають варіантами, а послідовність варіант, записаних у порядку зростання називають варіаційним рядом. Число спостережень кожної варіанти називають її частотою, а їх відношення до обсягу вибірки 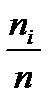- відносними частотами.

Означення:Статистичним розподілом вибірки називається перелік варіант та відповідних їм частот. Статистичний розподіл можна задати у вигляді послідовності інтервалів та відповідних їм частот (як частоту, що відповідає інтервалу, приймають суму частот, які попали в даний інтервал).

Приклад:

Дано статистичний розподіл вибірки

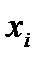
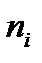
Записати розподіл відносних частот.

Рішення

За означенням відносної частоти 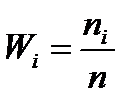, тоді враховуючи, що обсяг вибірки п=20:

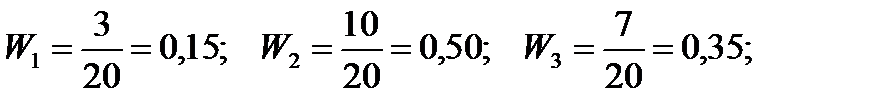
Тому статистичний розподіл відносних частот буде

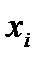
Розділ 11.2. Емпірична функція розподілу

Нехай відомий статистичний розподіл величини Х. п_х – число спостережень, при яких спостерігалося значення Х<x, n – загальне число спостережень (обсяг вибірки). Відносна частота події Х<x дорівнює 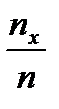. Якщо змінюється х , тоді змінюється і відносна частота, тобто відносна частота 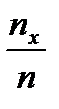є функцією від х. Оскільки ця функція знаходиться емпіричним (експериментальним) шляхом, то її називають емпіричною.

Означення: Емпіричною функцією розподілу називають функцію F^*(x), яка визначає для кожного значення х відносну частоту події Х<x.

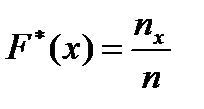, (11.1)

де п_х– число варіант, менших за х; п – обсяг вибірки.

<== попередня сторінка	\|	наступна сторінка ==>
Задачі до розділу 10.2	\|	Властивості емпіричної функції

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.