Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Оригінали та зображення.

Опорний конспект лекцій

з дисципліни Вища математика

для студентів заочної, прискореної форми навчання (ТСМ, ІМЗ)

(III курс, II семестр), лекція 5

Розділ 6. Основи операційного числення

Доцент к.ф.т.н. Плешівський Я.М.

Львів

2014р.

План лекції:

- поняття функції – оригіналів та зображення Лапласа;

- перетворення Лапласа та його основні властивості (зміна масштабу запізнення, диференціювання оригіналу та зображення, інтегрування оригіналу);

- розв’язування задач Коші для диференціальних рівнянь традиційним методом;

- основні поняття комбінаторики, теорії ймовірності;

- основні поняття та властивості теорії ймовірності, формули повної ймовірності;

- числові характеристики та закони розподілу неперервних випадкових величин (НВВ).

1. Поняття функції оригіналів та зображення Лапласа

Пер6творення Лапласа та його властивості є основою операційного числення, азбукою сучасної автоматики та телемеханіки. Вперше їх застосував в електротехнічних розрахунках англійський інженер – електрик О.Хевісайт.

Основна ідея операційного числення: мати функцію дійсної змінної f(t) (оригіналом) і функцію комплексної змінної F(p) (зображенням) встановлюється відповідність, яка дозволяє диференціювання та інтегрування оригіналу f(t) зводить до алгебраїчних операцій над зображенням F(p), тобто зводить розв’язок диференціальних, інтегральних, інтегро – диференціальних рівнянь до розв’язання алгебраїчних рівнянь.

Оригінали та зображення.

Озн.1. оригіналом називають функції f(t), які задовольняють умови:

- f(t) визначена для усіх 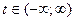, неперервна за виключенням можливо скінченної кількості точок розриву першого роду на кожному скінченному проміжку;

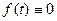- при 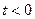(фізичний процес, який описує f(t), починається в момент часу ;

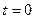- існують такі числа М та 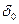, що

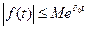(1) ( 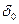-показник зростання )

Функції f(t)

Якщо f(t) обмежена, то 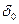=0.

Озн.2. Зображенням Лапласа оригіналу називають функцію F(p) комплексної змінної 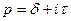, яку визначають за формулою

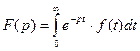
(2)

Відповідність між оригіналом f(t) і функцією F(p) встановлюється за допомогою перетворення Лапласа і позначається так :

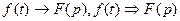або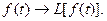

Теорема 1. Для будь – якого оригіналу f(t) зображення F(p) визначене і є аналітичною функцією в порівнянні .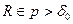

Одинична функція Хевісайда та її зображення :

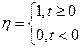
Ця функція визначена для усіх 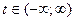неперервна з винятком точки t=0, обмеження і 1-3 умовам озн.1, є оригіналом

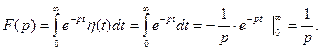
Таким чином : .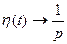

2. Властивості зображень Лапласа.

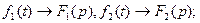
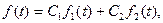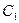1. Теорема про лінійність. Якщо де та 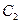- сталі , то 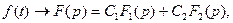тобто зображення лінійної комбінації оригіналів дорівнює відповідній лінійній комбінації їх зображень.

2. Теорема зміщення. Якщо 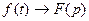і 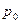- довільне комплексне число, то 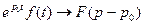для р таких, що 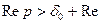, тобто зміщення зображення на 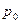рівносильне множенню оригіналу на .

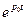Використовуючи ці властивості, знаходять зображення деяких функцій:

;

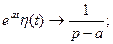
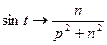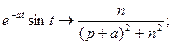
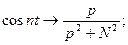
Теорема подібності. Якщо 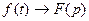, то для довільного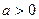

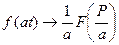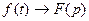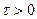Теорема запізнення. Якщо і , то

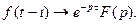
Приклад: 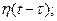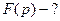Оскільки 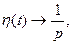то

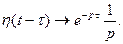
Теорема про диференціювання оригіналу. Якщо 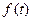n раз неперервно-диференційована на 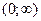і функції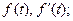 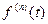є оригіналами, то із відповідності 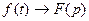випливає:

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

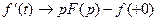
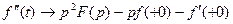
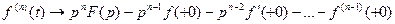
Зауваження: якщ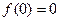о , то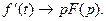

<== попередня сторінка	\|	наступна сторінка ==>
Співпраця з неурядовими організаціями	\|	Теорема про диференціювання зображення.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.