• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Метод множників Лагранжа. Умовні екстремуми функцій кількох змінних

Спочатку обмежимось функцією двох змінних:

.

(11.6)

На змінні 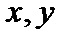накладена умова:

.

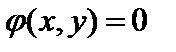(11.7)

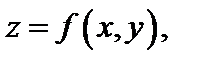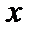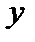Означення.Екстремум функції знайдений за умови (11.7), що певним чином зв’язує аргументи і , називається умовним екстремумом.

Для пошуку умовного екстремуму є два шляхи:

- виразимо із співвідношення (11.7) одну змінну, підставимо в формулу (11.6) і маємо задачу знаходження найбільшого і найменшого значень функції однієї змінної;

- якщо виразити одну змінну зі співвідношення (11.7) неможливо або недоцільно, застосовуємо так званий метод множників Лагранжа.

Розглянемо цей метод.

Вводимо допоміжну змінну 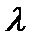і будуємо функцію Лагранжа.

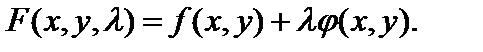
(11.8)

Сформуємо систему рівнянь для знаходження необхідних умов екстремуму:

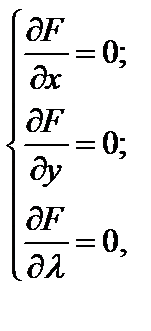
тобто

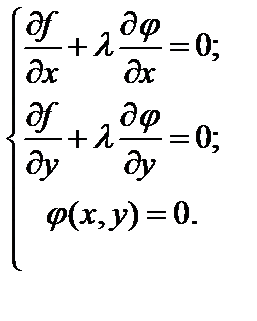
(11.9)

Із системи (1.4) знаходимо координати точок умовного екстремуму.

У загальному випадку маємо функцію 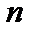змінних:

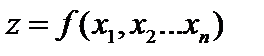
і 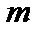умов:

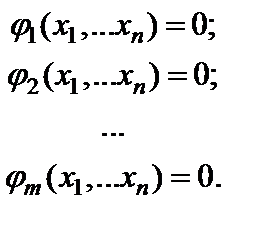
Вводимо функцію Лагранжа

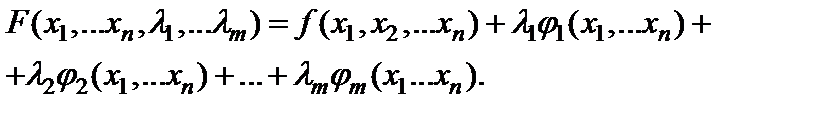
(11.10)

Координати точок умовного екстремуму знаходимо із системи рівнянь, ліва частина яких є частинні похідні функції (1.5) за змінними 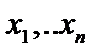і величинами .

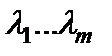Приклад 1.1. Треба знайти оптимальні розміри циліндричного баку для пального з умовою мінімізації загальної вартості будівельного матеріалу.

Умови задачі: об’єм баку 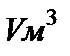, вартість 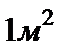матеріалу для бакових стінок дорівнює 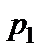, вартість 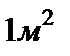для днища і покрівлі дорівнює .

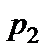Шукані величини: радіус основи 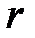і висота .

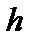Розв’язання. Функція, яку треба мінімізувати:

.

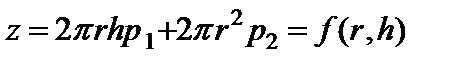Умова, яка відповідає співвідношенню (11.7):

.

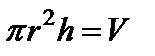Функція Лагранжа (1.3) має вигляд:

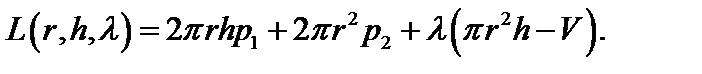
Застосуємо метод множників Лагранжа та складемо систему типу (11.9):

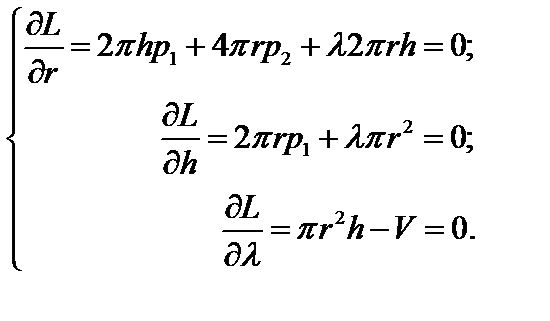
Із другого рівняння: 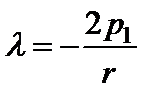. Підставимо у перше рівняння

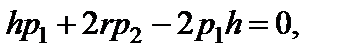або .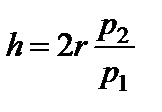

Підставимо значення 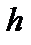у третє рівняння:

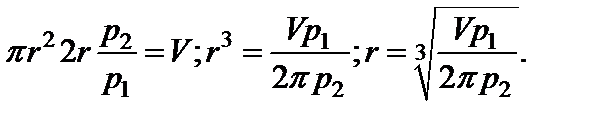
Звідси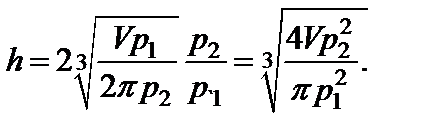

Шукані розміри знайдені.

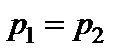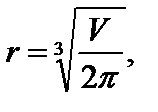
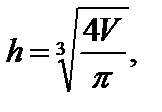
Частинний випадок: коли , то 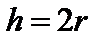, тобто бак має форму так званого рівностороннього циліндра, коли висота дорівнює діаметру.

Теорема Куна—Таккера

Розглянутий метод множників Лагранжа уможливлює знаходження лише локальних сідлових точок функції Лагранжа.

Теорема Куна—Таккера дає змогу встановити типи задач, для яких на множині допустимих розв’язків існує лише один глобальний екстремум зумовленого типу. Вона тісно пов’язана з необхідними та достатніми умовами існування сідлової точки.

Розглянемо задачу нелінійного програмування, яку, не зменшуючи загальності, подамо у вигляді:

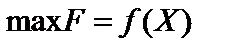, (11.12)

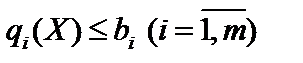, (11.13)

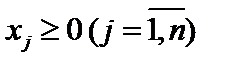. (11.14)

(Очевидно, що знак нерівності можна змінити на протилежний множенням лівої і правої частин обмеження на (– 1)).

Теорема 8.1. (Теорема Куна—Таккера). Вектор Х^* є оптимальним розв’язком задачі (11.12)—(11.14) тоді і тільки тоді, коли існує такий вектор , що при 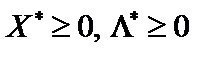для всіх 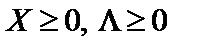точка 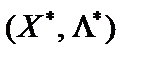є сідловою точкою функції Лагранжа

,

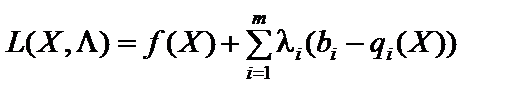і функція мети 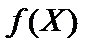для всіх 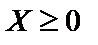угнута, а функції 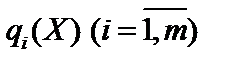— опуклі.

Умови теореми Куна — Таккера виконуються лише для задач, що містять опуклі функції.

Опуклі й угнуті функції

Наведемо основні означення та теореми. Нехай задано n-вимірний лінійний простір Rⁿ. Функція 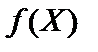, що задана на опуклій множині 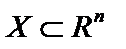, називається опуклою, якщо для будь-яких двох точок 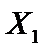та 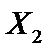з множини X і будь-яких значень 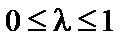виконується співвідношення:

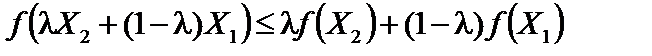. (11.17)

Якщо нерівність строга і виконується для 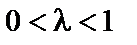, то функція 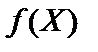називається строго опуклою.

Функція 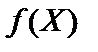, яка задана на опуклій множині ,
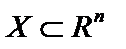називається угнутою, якщо для будь-яких двох точок 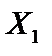та 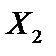з множини X і будь-якого 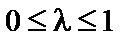справджується співвідношення:

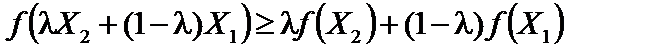. (11.18)

Якщо нерівність строга і виконується для 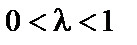, то функція 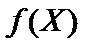називається строго угнутою.

Слід зазначити, що опуклість та угнутість функції визначаються лише відносно опуклих множин у 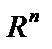, оскільки за наведеними означеннями разом з двома будь-якими точками та множині X належать також точки їх лінійної комбінації: 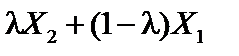для всіх значень 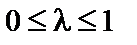, що можливо лише у разі, коли множина X є опуклою.

Теорема. Нехай 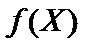— опукла функція, що задана на замкненій опуклій множині X, тоді будь-який локальний мінімум 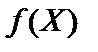на цій множині є і глобальним.

Доведення. Допустимо, що в точці 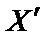функція 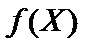має локальний мінімум, тоді як глобальний мінімум досягається в точці 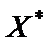, отже, виконуватиметься нерівність 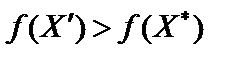. Через те що 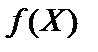— опукла функція, для будь-яких значень 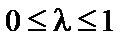справджується співвідношення:

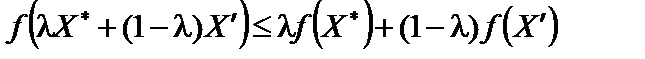. (11.19)

Множина Х опукла, тому точка 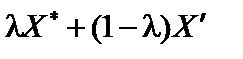при також належить цій множині. Враховуючи, що 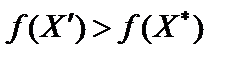, нерів­ність (11.19) матиме вигляд:

;

.

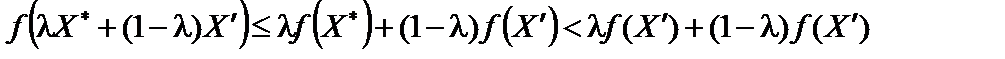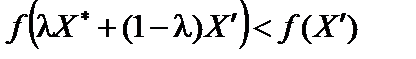Значення 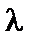можна вибрати так, щоб точка 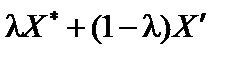була розташована як завгодно близько до 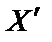. Тоді отримана остання нерівність суперечить тому, що 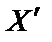— точка локального мінімуму, оскільки існує як завгодно близька до неї точка, в якій функція набуває меншого значення, ніж у точці 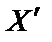. Тому попереднє допущення неправильне. Теорему доведено.

Теорема. Нехай 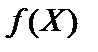— опукла функція, що визначена на опуклій множині Х, і крім того, вона неперервна разом з частинними похідними першого порядку в усіх внутрішніх точках Х. Нехай 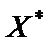— точка, в якій 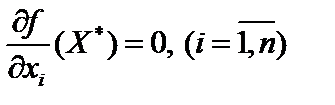. Тоді в точці 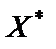досягається локальний мінімум, що збігається з глобальним.

Як наслідок теореми можна показати, що коли Х замкнена, обмежена знизу, опукла множина, то глобального максимуму опукла функція f(X) досягає на ній у одній чи кількох точках (при цьому допускається, що в точці Х значення функції скінченне). Застосовуючи за розв’язування таких задач процедуру перебору крайніх точок, можна отримати точку локального максимуму, однак не можна встановити, чи є вона точкою глобального максимуму.

Для угнутих функцій отримані результати формулюють так. Нехай f(X) — угнута функція, що задана на замкненій опуклій множині 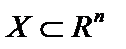. Тоді будь-який локальний максимум f(X) на множині Х є глобальним. Якщо глобальний максимум досягається в двох різних точках множини, то він досягається і на нескінченній множині точок, що лежать на відрізку, який сполучає ці точки. Для строго угнутої функції існує єдина точка, в якій вона досягає глобального максимуму.

Градієнт угнутої функції f(X) у точках максимуму дорівнює нулю, якщо f(X) — диференційовна функція. Глобальний мінімум угнутої функції, якщо він скінченний на замкненій обмеженій зверху множині, має досягатися в одній чи кількох її крайніх точках за умови скінченності функції f(X) у кожній точці цієї множини.

Переглядів: 1787