Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Постановка задачі

Так звана транспортна задача (ТЗ) є частинним випадком загальної задачі лінійного програмування. Її прості в математичному аспекті умови дозволяють застосувати значно більш ефективні методи розв’язування, ніж для загальної задачі.

Один із варіантів постановки ТЗ полягає у знаходженні оптимального плану перевезень деякого однорідного вантажу з 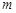пунктів виробництва або складі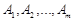в в 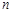пунктів призначення (споживання) .

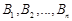Оптимізація плану перевезень полягає у мінімізації загальної вартості перевезень або мінімального часу їх доставки.

Сформулюємо математичну постановку цього варіанту задачі (з мінімізацією загальної вартості).

Задано:

- обсяги виробництва (запаси), що дорівнюють 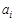, у пунктах , ;

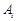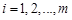- обсяги споживання (заявки), що дорівнюють 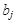, у пунктах , ;

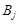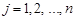- матриця , де 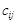– затрати на перевезення одиниці вантажу з пункту 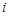до пункту .

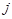Треба знайти множину 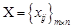, що містить 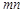значень 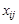, де 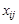- обсяг перевезень з пункту 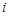в пункт 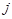, таку, що мінімізує функцію

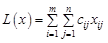
(1.1)

за умов:

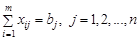(1.2)

(задоволення всіх заявок);

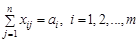(1.3)

(реалізація всіх запасів)

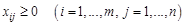(1.4)

(зворотні перевезення від 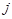до 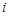усуваються).

У найпростішому варіанті повинна виконуватися ще умова рівності суми заявок і запасів:

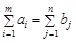. (1.5)

Цю умову можна записати ще й так:

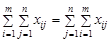, (1.6)

звідки видно, що одне з рівнянь систем (1.2) і (1.3) не є незалежним, оскільки є наслідком решти.

У цьому варіанті задача називається закритою. Якщо умова (1.5) не виконується, задача називається відкритою. Вона легко зводиться до закритої.

Означення. Множина 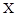, що задовольняє умови (1.2), (1.3), (1.4), називається допустимим планом. Легко бачити, що ранг матриці системи рівнянь (1.2) і (1.3) у невиродженому випадку дорівнює 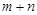, але умова (1.5) або (1.6) зменшує ранг на одиницю, і таким чином ранг системи (1.2), (1.3), (1.6) дорівнює 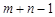. Звідси в системі може бути 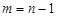базисних змінних. Кількість вільних змінних дорівнює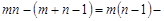 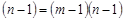. Розглядаючи загальну ЗЛП (п. 2.5), видно, що в оптимальному плані вільні змінні повинні дорівнювати нулю.

Означення. Допустимий план, у якому не більше, як 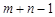ненульових величин 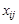, називається базисним або опорним.

Означення. Базисний план, що мінімізує функцію (1.1), називається оптимальним.

Твердження. На відміну від загальної задачі ЛП, ТЗ завжди має допустимий і оптимальний плани.

<== попередня сторінка	\|	наступна сторінка ==>
Метод множників Лагранжа. Умовні екстремуми функцій кількох змінних	\|	Розв’язування транспортної задачі

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.