
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Роз'вязування систем лінійних рівнянь за формулами Крамера
Мета теми:навчитися розв'язувати системи лінійних рівнянь за допомогою формул Крамера
Студент повинен знати: означення визначника третього та n порядків, властивості; теорему про розкладання визначника. Формули Крамера для систем 2-х,3-х лінійних рівнянь з 2-ма,3-ма змінними; кількість розв'язків системи залежно від значень визначників системи.
Студент повинен вміти:обчислювати визначники другого, третього та четвертого порядків; застосовувати теорему про розкладання визначника за елементами рядків та стовпчиків для обчислювання визначників. Застосовувати формули Крамера для розв'язування систем лінійних рівнянь
Основні питання теми:
1.Означення визначника 2, 3 та n порядку.
2.Загальний вигляд визначника n порядку.
3.Властивості визначників.
4.Формули Крамера для систем двох лінійних рівнянь.
5.Формули Крамера для систем трьох лінійних рівнянь.
6.Умови існування розв'язків системи.
7.Приклади розв'язання систем.
Свої набуті знання ви можете перевірити за наступними питаннями
1.Який вигляд має система 2-х, 3-х лінійних рівнянь з двома, трьома змінними?
2.Що таке головний визначник системи?
3.Який вигляд мають формули Крамера?
4.Коли система має єдиний розв'язок?
5.Коли система має безліч розв'язків?
6.Коли система не має розв'язків?
7.Чи можна застосовувати формули Крамера для будь-якої системи лінійних рівнянь?
Завдання для самоперевірки
Розв’язати за формулами Крамера системи рівнянь
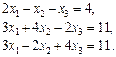
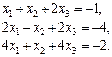
Відповідь. 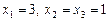 . Відповідь.
. Відповідь. 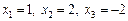 .
.
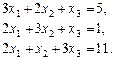
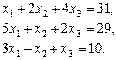
Відповідь. 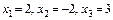 . Відповідь.
. Відповідь. 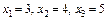 .
.

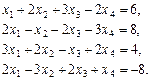
Відповідь. 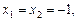 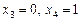 . .
| Відповідь. 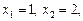 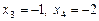 . .
|
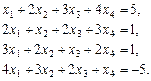
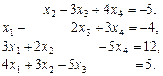
Відповідь. 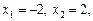 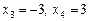 . .
| Відповідь. 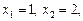 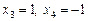 . .
|
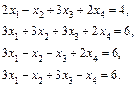
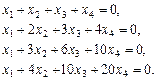
Відповідь. 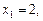 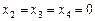 . .
| Відповідь. 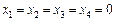 . .
|
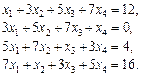
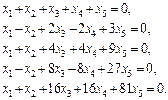
Відповідь. 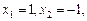 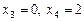 . .
| Відповідь. 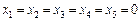 . .
|
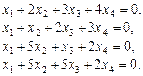

Відповідь. 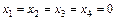 . Відповідь.
. Відповідь. 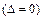 .
.
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,
стор.21 – 23.
Лекція ” Формули Крамера”
Спинимося на застосуванні теорії визначників до розв’язування системи n лінійних алгебраїчних рівнянь з n невідомими:
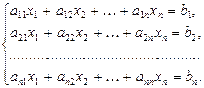 (1)
(1)
Означення. Визначник, елементами якого є коефіцієнти при невідомих у системі (1)
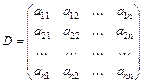 , (2)
, (2)
називається визначником цієї системи.
Теорема. Якщо визначник D системи лінійних алгебраїчних рівнянь (1) відмінний від нуля, то ця система має єдиний розв’язок:
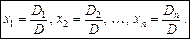 (3)
(3)
ТутDk— визначник, утворений з визначникаDсистеми (1) заміною k-го стовпця на стовпець із правих її частин.
Доведення. Помноживши k-те рівняння системи (1) на алгебраїчне доповнення Aks елемента аks і додавши всі рівняння, дістанемо:
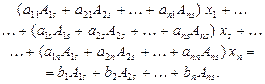
Згідно з властивостями 9 і 10 визначників маємо рівняння
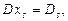
з якого при 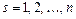 випливають формули (3).
випливають формули (3).
Отже, якщо система рівнянь (1) має розв’язок, то він подається у вигляді (3).
Доведемо, що ці формули справді визначають розв’язок системи рівнянь (1), підставивши туди розв’язки (3). Для k-го рівняння маємо:
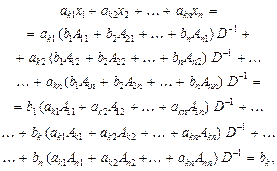
з якого випливає справедливість теореми. ¨
Приклад. Розв’яжемо за формулами Крамера систему рівнянь:
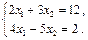
· Запишемо відповідні визначники і знайдемо розв’язки системи рівнянь:
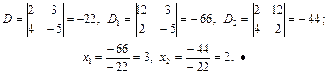
Приклад. Розв’яжемо систему рівнянь
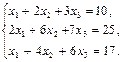
· Обчислимо визначник цієї системи:
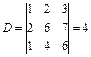 .
.
Визначник системи відмінний від нуля. Знайдемо тепер визначник 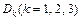 і розв’язки системи рівнянь:
і розв’язки системи рівнянь:
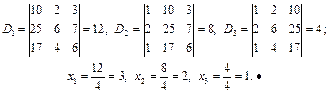
Формули Крамера незручні для практичних обчислень при 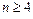 , але вони застосовуються в теоретичних дослідженнях.
, але вони застосовуються в теоретичних дослідженнях.
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001
Тема 3
| <== попередня сторінка | | | наступна сторінка ==> |
| Властивості визначників | | | Ранг матриці. Умови сумісності та визначеності СЛР |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |