Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розглянемо систему однорідних рівнянь

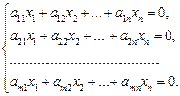(1)

Теорема 3. Для того щоб однорідна система лінійних алгебраїчних рівнянь (1) мала єдиний нульовий розв’язок 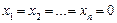, необхідно і достатньо, щоб при 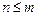дефект матрицікоефіцієнтів цієї системи дорівнював нулю.

Іншими словами, система лінійних однорідних рівнянь (1) має лише нульовий розв’язок, якщо ранг матриці А дорівнює n.

Теорема 4. Для того щоб однорідна система рівнянь (1) мала ненульовий розв’язок, необхідно і достатньо, щоб ранг матриці А був меншим від n.

Оскільки при 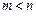ранг матриці А не може бути більшим за m, то при 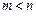система однорідних рівнянь (1) є невизначеною і завжди має ненульовий розв’язок.

Теорема 5. Якщо ранг r матраці А менший за n, то загальне число лінійно незалежних ненульових розв’язків системи (1) дорівнює дефекту матриці: .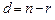

При цьому загальні розв’язки системи (1) можна подати у вигляді

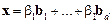де 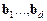— лінійно незалежні розв’язки системи рівнянь .

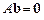Розглянемо тепер неоднорідну систему лінійних алгебраїчних рівнянь

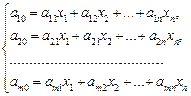(3)

Теорема 6. (Кронекера—Капеллі). Для того щоб неоднорідна система лінійних алгебраїчних рівнянь (3) була сумісною, необхідно і достатньо, щоб ранг матриці А дорівнював рангу розширеної матриці

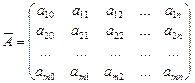Доведення. Якщо 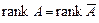, то перший стовпець матриці 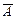є лінійною комбінацією решти її стовпців,аотже, система рівнянь (3) має розв’язки.

Коли система (3) має розв’язки, то перший стовпець матриці 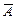є лінійною комбінацією решти її стовпців. Звідси випливає, що матриц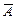і і 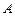містять однакове число лінійно незалежних стовпців. Отже, 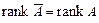, що й доводить теорему. ¨

Загальний розв’язок системи рівнянь (3) складається з частинного розв’язку системи (3) та загального розв’язку однорідної системи (1). Таким чином, очевидними є наведені далі теореми.

Теорема 7. Для того щоб неоднорідна система рівнянь (3) мала єдиний розв’язок, необхідно, щоб .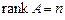

Теорема 8. Нехай 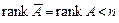. Система неоднорідних рівнянь (3) має загальний розв’язок виду

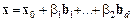де 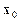— частинний розв’язок неоднорідної системи рівнянь (3), а 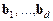— лінійно незалежні розв’язки однорідної системи .

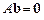Можна дійти висновку, що коли число m рівнянь у системі (3) менше за число невідомих n, то ця система або невизначена, або суперечлива.

Приклад. Система рівнянь 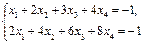є несумісною.

· Справді, якщо перше рівняння помножимо на 2 і віднімемо від другого рівняння, дістанемо неможливу числову рівність 0 = 1. ·

Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,

стор.18 – 19, 30 – 31.

Розділ „Елементи векторної алгебри та

аналітичної геометрії”

Тема 4

Вектори і лінійні дії над ними. Розклад вектора за базисом. Координати вектора, довжина вектора, дії над векторами, що задаються своїми координатами. Обчислення скалярного добутку та косинуса кута між двома векторами.

Мета заняття Узагальнення та систематизація знань з даної теми, повторення формул стереометрії.

Розвивати просторове мислення.

Студенти повинні знати: означення вектора та лінійні дії над ними; поняття про базис вектора; основні формули дій над векторами, які задані координатами, означення направляючих косинусів; означення скалярного добутку у просторі, та косинуса кута між векторами;

Студенти повинні вміти: виконувати лінійні дії над векторами; розкладати вектор за базисом; виконувати дії над векторами, які задані координатами; обчислювати скалярний добуток двох векторів на площині і у просторі.

Основні питання теми

1.Скалярні та векторні величини; дії над векторами;

2.Розклад вектора за базисом на площині та у просторі; координати вектора;

3.Формули для обчислення довжини вектора;

4.Скалярний добуток двох векторів та його властивості;

5.Обчислення кута між двома векторами;

<== попередня сторінка	\|	наступна сторінка ==>
Свої набуті знання ви можете перевірите в наступному тесті	\|	Свої набуті знання ви можете перевірити в наступному тесті

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.