
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Свої набуті знання ви можете перевірити в наступному тесті
1.Відрізок, що має певну довжину і певний напрямок називається...
а)промінем б)вектором
в)хордою г)медіаною
2.Одиничний вектор,напрям якого збігається з даним вектором, називається...
а)0-вектором б)вектор-сумою
в)модулем вектора г)ортом
3.Якщо 2 вектора лежать на одній прямій, або на паралельних прямих, вони називаються...
а)компланарними б)скалярними
в)рівними г)колінеарними
4.Якщо 3 вектора лежать в одній площині або в паралельних площинах, вони називаються...
а)компланарними б)скалярними
в)рівними г)колінеарними
5.Довільна упорядкована пара неколінеарних векторів називається... на площині
а)ортом б)комбінацією
в)основою г)базисом
6.Довільна упорядкована трійка некомпланарних векторів називається у просторі
а)ортом б)комбінацією
в)основою г)базисом
7.Коефіциєнти, що стоять біля векторів базису в розкладанні вектора за базисом називаються в даному базисі...
а)ортами вектора б)системою вектора
в)координатами вектора г)проекцією вектора
8.Добуток довжин двох векторів на косинус кута між ними називається...
а)кутовим добутком б)мішаним добутком
в)векторним добутком г)скалярним добутком
Завдання для самоперевірки
1.Довести, що вектори а = (3;-2;1), b = (-1;1;-2), с = (2;1;-3) і d = (11;-6;5) лінійно залежні. Виразити вектор d як лінійну комбінацію векторів а, b i с.
2.Відомо, що вектор а = (0;-2;-3) і b = (3;2;3). Переконатись,що |3а + 2b| = 7.
3.Знайти координати векторів, їхню довжину та кути між ними, якщо вони задані в системі координат на малюнку. Довжина сторони правильного шестикутника дорівнює 4.
4.Визначити скалярний добуток векторів х і y:
a) 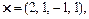
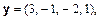
б) 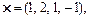
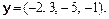
Відповідь. а) 9; б) 0.
5.Визначити кут між векторами х і y:
a) 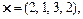
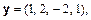
б) 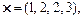
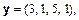
в) 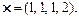
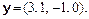
Відповідь. а) 90°; б) 45°; в) 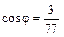 .
.
6.Закінчте вирази:
1). Вектором називається …
2). Вектори вважаються рівними, якщо …
3). З векторами виконуються такі лінійні операції: …, за правилами…
4). Лінійні операції над векторами мають такі властивос-
ті: …
5). Проекцією вектора на вісь називається …
6). Проекція добутку вектора на скаляр дорівнює …
7). Проекція суми векторів дорівнює …
7. Перевірити за допомогою паралелограма, побудованого на векторах 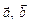 , справджуваність таких тотожностей:
, справджуваність таких тотожностей:
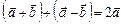 ;
; 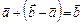 ;
;
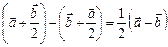 ;
; 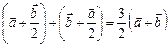 .
.
8. На сторонах ОА і ОВ прямокутника ОАСВ відкладено одиничні орти 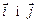 . Виразити через них вектори
. Виразити через них вектори 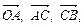
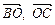 і
і 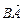 , якщо довжина
, якщо довжина 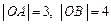 .
.
9. Три вектори 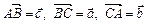 є сторонами трикутника. За допомогою векторів
є сторонами трикутника. За допомогою векторів 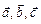 виразити медіани трикутника
виразити медіани трикутника 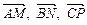 .
.
10. У рівнобічній трапеції ОАСВ кут ВОА = 60°, ОВ = ВС =
= СА = 2, М і N — середини сторін ВС і АС. Виразити вектори 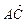 ,
, 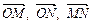 через
через 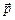 і
і 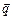 — одиничні вектори напрямів
— одиничні вектори напрямів 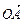 і
і 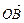 .
.
11. Сторона ВС трикутника розділена на п’ять рівних
частин точками 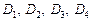 , які з’єднані з вершиною А. Вектори
, які з’єднані з вершиною А. Вектори 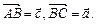 Знайти вирази для векторів
Знайти вирази для векторів 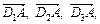
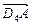 .
.
12. В ромбі ABCD дано діагоналі 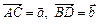 . Розкласти за цими векторами всі вектори, що збігаються зі сторонами ромба:
. Розкласти за цими векторами всі вектори, що збігаються зі сторонами ромба: 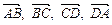 .
.
13. У правильному шестикутнику ABCDEF дано: 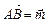
і 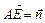 . Розкласти за цими векторами вектори
. Розкласти за цими векторами вектори 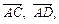
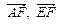 .
.
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001
гл. , стор.32 – 57.
Лекція” Вектори, лінійні операції над векторами”
Означення. Векторною величиною, або вектором (у широкому розумінні), називається будь-яка величина, що має напрям (наприклад, сила, що діє на матеріальну точку).
Означення. У геометрії вектором (у вузькому розумінні) називається напрямлений відрізок. Напрям відрізка вказується стрілкою. Розрізняють початок і кінець вектора.
Означення. Два вектори називаються рівними між собою, якщо кожний із них можна дістати паралельним перенесенням іншого.
Рівні вектори є паралельними (колінеарними), мають один і той самий напрям і однакову довжину. Довжина вектора а називається також абсолютною величиною, або модулем, вектора і позначається 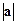 .
.
Означення. Вектор називається нульовим (нуль-вектором), якщо він має нульову довжину, тобто його кінець збігається з початком.
На письмі вектор позначається напівжирним шрифтом.
Щоб знайти суму двох векторів а і b, сумістимо початок вектора b з кінцем вектора а.
Означення. Сумою a + b векторів a та b називається вектор, початок якого збігається з початком вектора a, а кінець — із кінцем вектора b (мал. 1).

Мал. 1 Мал. 2
Додавання векторів комутативне, тобто для довільних векторів a і b справджується рівність (мал. 2)
a + b = b + a. (1)
Додавання векторів асоціативне, тобто для будь-яких векторів a,b,c виконується рівність
(a + b) + c = a +(b + c). (2)
Цю властивість, що випливає з означення суми векторів, унаочнює мал. 3.
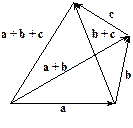
Мал.3
Віднімання векторів — операція, обернена до їх додавання. Різниця b – a векторів a і b являє собою вектор, початок якого збігається з початком вектора a, а кінець — із кінцем вектора b (мал. 4).
a +(b – a) = b
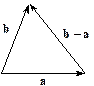
мал. 4
Для будь-яких векторів a, b виконуються нерівності:
 .
.
Розглянемо довільний вектор a і вісь х.
Означення. Якщо вектор a утворює кут j з віссю х (мал. 5), то проекцією вектора а на вісь називається величина
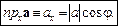 . (3)
. (3)
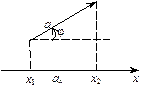
Мал.5
Якщо х1 — координата проекції початку вектора, а х2 — координата проекції кінця вектора на вісь х, то
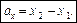 (4)
(4)
Нехай вектор а має початок у точці М1(х1, y1, z1), а кінець — у точці М2(х2, y2, z2). Тоді величини
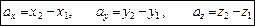
є проекціями вектора a на осі х, y, z. Проекції вектора однозначно визначають вектор. Тому виконується рівність
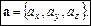
Очевидно, що проекція на вісь х суми a + b векторів a та b дорівнює сумі проекцій на вісь х векторів a, b(мал. 6).
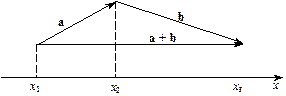
Мал.6
● Справді, виконуються рівності
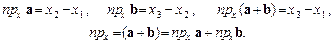
Нехай відомі проекції векторів a та b:
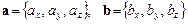 .
.
Тоді проекція суми векторів a + b дорівнює сумі відповідних проекцій векторів-доданків:
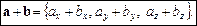
Означення. Добутком вектораaна числоl називається вектор 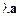 , довжина якого дорівнює
, довжина якого дорівнює 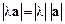 . Вектор
. Вектор 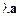 колінеарний вектору а; має однаковий з ним напрям при
колінеарний вектору а; має однаковий з ним напрям при 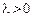 і протилежний напрям при
і протилежний напрям при 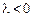 . Якщо
. Якщо 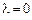 або
або 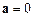 , то маємо
, то маємо 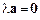 , тобто добуток є нуль-вектором.
, тобто добуток є нуль-вектором.
Множення вектора на число має властивість асоціативності та дистрибутивності. Для довільних чисел l, m та векторів a, b справджуються рівності:
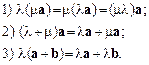 (5)
(5)
Останню рівність унаочнює мал. 7 ( 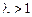 ).
).
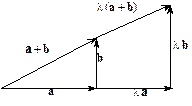 Мал.7
Мал.7
Ця властивість випливає з подібності трикутників із коефіцієнтом подібності l.
З очевидної рівності
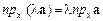
випливає:
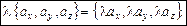
Лема. Будь-який вектор a можна єдиним чином подати у вигляді суми трьох векторів, кожний із яких колінеарний одній з осей координат х, у, z.
¨ Справді, нехай М1 — початок вектора a, М2 — його кінець. Сумістимо точку М1 із початком координат. Опустимо з точки М2 перпендикуляр на координатну площину ху і позначимо здобуту проекцію М3. Із точки М3 опустимо перпендикуляр на вісь х. Відповідну проекцію позначимо М4. Вектор М3М2 колінеарний осі z, вектор М4М3 — осі у, а вектор М1М4 — осі х.
Звідси, скориставшись одиничними векторами i, j, k, що, як відомо, колінеарні осям х, у, z, дістанемо:
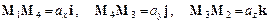 .
.
Оскільки виконується рівність 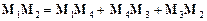 (мал. 8),
(мал. 8),
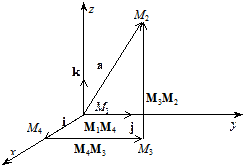
Мал.8
то вектор a можна записати у вигляді:
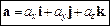 (6)
(6)
Вектори 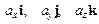 називаються координатами вектора a.
називаються координатами вектора a.
Приклад. Дано два вектори:
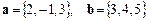 .
.
Знайдемо за формулою (6) вектор
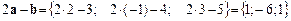 .
.
Скалярний добуток векторів
Означення. Скалярним добутком векторів a і b називається число 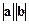 , що дорівнює добутку довжини цих векторів на косинус кута між ними (мал. 9):
, що дорівнює добутку довжини цих векторів на косинус кута між ними (мал. 9):
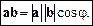 (1)
(1)
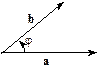 Мал.9
Мал.9
Нехай 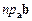 — проекція вектора b на вісь, паралельну вектору a. Тоді маємо:
— проекція вектора b на вісь, паралельну вектору a. Тоді маємо:
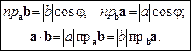 (2)
(2)
Останнє співвідношення означає, що скалярний добуток двох векторів дорівнює модулю одного з них, помноженому на проекцію другого вектора на напрям першого.
Якщо кут між векторами a та b гострий, то 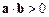 ; якщо тупий, то
; якщо тупий, то 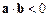 ; якщо прямий, то
; якщо прямий, то 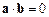 . Коли один із векторів a, bє нульовим, то його можна вважати ортогональним до будь-якого іншого вектора.
. Коли один із векторів a, bє нульовим, то його можна вважати ортогональним до будь-якого іншого вектора.
Наведемо аналітичні властивості скалярного добутку, що випливають із його означення.
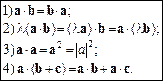
Остання рівність є наслідком формули (2) і властивості проекцій суми векторів:
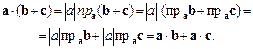
Отже, у разі скалярного множення суми векторів на вектор можна розкривати дужки. Нехай вектори а та b подано через їх проекції на координатні осі:
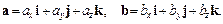
Запишемо таблицю скалярного множення для одиничних векторів i, j, k — ортів системи координат:
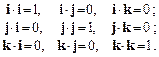
Перемноживши скалярно вектори a та b, знайдемо їх скалярний добуток у проекціях на координатні осі:
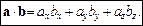 (3)
(3)
Звідси маємо:
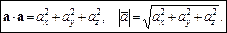
Знаючи проекції векторів а, b, можна знайти кут між цими векторами:
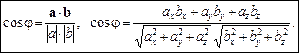
Приклад. Дано просторовий трикутник з вершинами А(1, 2, –1),
В(2, 4, 1), С(3, 0, 0). Знайдемо кут при вершині А.
· Розглянемо вектори
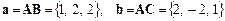
і з їх скалярного добутку визначимо косинус шуканого кута:
 .
.
Оскільки скалярний добуток векторів a, bдорівнює нулю, то кут при вершині А прямий. ·
Властивості додавання векторів та множення числа на вектор (l, m — деякі числа):
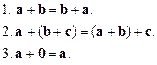
4. Для будь-якого вектора а існує протилежний вектор –а, такий що 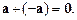
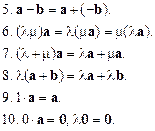
Із означення скалярного добутку випливають такі його властивості:
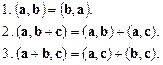
Зауваження. Скалярному добутку можна дати економічну інтерпретацію, розглянувши m різних товарів відповідно кількістю  та ціною
та ціною 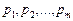 за одиницю товару. Загальну вартість усіх товарів можна подати скалярним добутком вектора кількості товарів
за одиницю товару. Загальну вартість усіх товарів можна подати скалярним добутком вектора кількості товарів 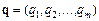 і вектора цін
і вектора цін 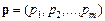 :
:
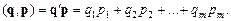
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001
гл.2, §1- 4, стор.32 – 57.
Тема 5
Різні види рівнянь прямої на площині
Мета заняття Вивчити різні види завдань прямої на площині та відповідні їм рівняння. Розвивати просторове мислення.
Студенти повинні знати: означення напрямного та нормального векторів прямої; різні види рівнянь прямої на площині.
Студенти повинні вміти: знаходити різні види рівнянь прямої на площині відповідно способам завдання.
Основні питання теми
При вивченні цієї теми треба спочатку уважно прочитати матеріал, зробити конспект, в якому повинні бути зображені різні способи завдання проямої і записані відповідні їм рівняння. Це зручно зробити за наступним планом:
1.Поняття нормального та напрямного векторів прямої;
2.Пряма, що проходить через дану точку і має заданий напрямний вектор;
3.Пряма, що проходить через дві дані точки;
4.Пряма, що відрізає на осях координат задані відрізки;
5.Пряма, що проходить через дану точку і має заданий нормальний вектор;
6.Пряма що проходить через дану точку і має даний кутовий коефіциент;
Завдання для самоперевірки
Скласти рівняння прямої, що проходить:
1)через точки А(-4;3) і В(2;-1);
2)через точку М(5;3) паралельно прямій 2х – 4у = 7;
3)через точку Р(3;-4) під кутом° 30 до осі ОХ.
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,
стор.76 – 80.
Лекція ”Пряма лінія на площині”
Нехай на площині задано пряму у прямокутній системі координат х, у. Кут j між віссю Ох і цією прямою називається кутом нахилу прямої до осі. Тангенс кута нахилу 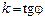 називається кутовим коефіцієнтом розглядуваної прямої. Якщо ця пряма перетинає вісь Оу у точці В з координатами (0, b), то число b називається початковою ординатою. Візьмемо довільну точку М(х, у) на прямій (мал. 1).
називається кутовим коефіцієнтом розглядуваної прямої. Якщо ця пряма перетинає вісь Оу у точці В з координатами (0, b), то число b називається початковою ординатою. Візьмемо довільну точку М(х, у) на прямій (мал. 1).
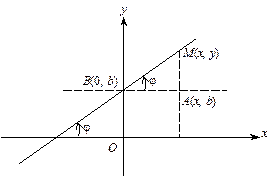 Мал. 1
Мал. 1
З прямокутного трикутника МАВ знаходимо рівняння прямої
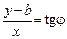 ,
,
яке можна подати у вигляді
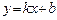 , де , де 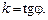
| (1) |
Якщо розглядувана пряма паралельна осі Оу, то j = 0,5p і tgj не існує. При цьому пряма має рівняння виду х = а (мал. 2).

мал. 2
Координати х, у будь-якої точки М(х, у), що належить прямій, задовольняють рівняння (1). Якщо пряма (1) проходить через точку М1(х1, у1), то справджується рівність
у1 = kx1 + b,
Віднімаючи почленно цю рівність від рівності (1), дістаємо рівняння прямої, що проходить через задану точку:
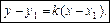 (2)
(2)
Зі зміною кутового коефіцієнта k в рівнянні (2) утворюються різні прямі, що проходять через точку М1(х1, у1). Рівняння (2) називається рівнянням пучка (в’язки) прямих (мал. 3).
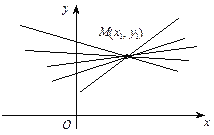
Мал. 3
Нехай дано дві різні точки М1(х1, у1), М2 (х2, у2), де х2 ¹ х1. З рівняння (2) випливає вираз для кутового коефіцієнта прямої, що проходить через точки М1, М2:
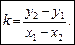 (3)
(3)
Підставляючи в (3) рівняння (2), знаходимо рівняння прямої, що проходить через дві задані точки М1(х1, у1), М2 (х2, у2):
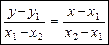 (4)
(4)
Приклад. Знайдемо рівняння прямої, що проходить через дві точки М1(4, 1), М2(2, 3).
· Згідно з (4) маємо:
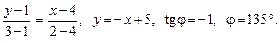
Ця пряма утворює кут 135° з віссю Ох. ·
Якщо задано вектор 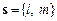 , паралельний деякій прямій, і точку М0(х0, у0) на цій прямій, то рівняння прямої можна записати у вигляді
, паралельний деякій прямій, і точку М0(х0, у0) на цій прямій, то рівняння прямої можна записати у вигляді
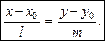
Вектор s називається напрямним вектором прямої.
Щоб побудувати графік прямої, достатньо знати дві її різні точки і через них провести пряму. Якщо пряма перетинає осі координат у точках М1(а, 0), М2(0, b), а ¹ 0, b ¹ 0, то її можна записати рівнянням
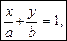 (5)
(5)
яке називається рівнянням прямої у відрізках на осях.
Приклад. Запишемо рівняння прямої

у вигляді (5).
· Значенню у1 = 0 відповідає х1 = 3. При х2 = 0 знаходимо у2 = 2. Отже, шукане рівняння прямої подається у вигляді
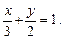
Пряма перетинає вісь х у точці з координатою х = 3, а вісь у — у точці з координатою у = 2. ·
Розглянемо на площині прямокутну систему координат х, у і знайдемо рівняння прямої, коли відомий вектор її нормалі 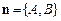 і задано точку М0(х0, у0) на цій прямій. Нехай М(х, у) — довільна точка шуканої прямої (мал. 4).
і задано точку М0(х0, у0) на цій прямій. Нехай М(х, у) — довільна точка шуканої прямої (мал. 4).
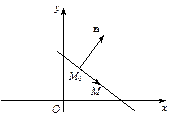
мал. 4
За умовою вектор 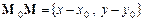 перпендикулярний до вектора
перпендикулярний до вектора 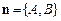 . Тому їх скалярний добуток
. Тому їх скалярний добуток 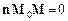 . Звідси маємо рівняння
. Звідси маємо рівняння
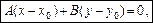 (1)
(1)
або
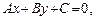 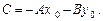
| (2) |
Це рівняння називається загальним рівнянням прямої.
На відміну від рівняння виду (1) змінні х, у входять до рівняння (2) рівноправно. Рівняння (1) завжди можна подати у вигляді (2).
Рівняння прямої (2) можна записати у вигляді (y = kx + b) лише за умови В ¹ 0.
Коефіцієнти А, В при х, у у загальному рівнянні прямої є про-
екціями на координатні осі вектора її нормалі n.
Справджується теорема.
Теорема 1. Будь-яка пряма на площині може бути задана лінійним рівнянням виду (2). Кожне лінійне рівняння виду (2), деА2 + В2 > 0,визначає деяку пряму.
Доведення. Перше твердження теореми було доведено раніше при виведенні рівняння (1). Доведемо друге твердження. Візьмемо довільне лінійне рівняння
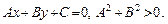
Оскільки коефіцієнти при х, у не перетворюються одночасно на нуль, завжди знайдуться значення х = х0, у = у0, при яких виконується рівність
Ах0 + Ву0 + С = 0.
Віднімаючи ці рівняння почленно, дістаємо рівність
А(х – х0) + В(у – у0) = 0. (3)
За допомогою векторів
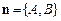 ,
, 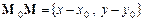
рівність (3) можна записати у вигляді 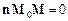 .
.
Як бачимо з мал.4, вектор 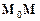 тоді і тільки тоді буде перпендикулярним до ненульового вектора
тоді і тільки тоді буде перпендикулярним до ненульового вектора 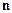 , коли точка М(х, у) лежить на прямій, що проходить через точку М0(х0, у0) перпендикулярно до цього вектора. Звідси випливає рівняння (1), що визначає деяку пряму. Отже, теорему доведено. ¨
, коли точка М(х, у) лежить на прямій, що проходить через точку М0(х0, у0) перпендикулярно до цього вектора. Звідси випливає рівняння (1), що визначає деяку пряму. Отже, теорему доведено. ¨
Нехай х, у — координати довільної точки на площині. Пряма (2) поділяє всю площину на дві півплощини. В одній півплощині виконується нерівність Ах + Ву + С > 0, а в іншій — нерівність
Ах + Ву + С < 0. На самій прямій маємо: Ах + Ву + С = 0.
Розглянемо частинні випадки рівняння (2):
якщо А = 0, то пряма паралельна осі х;
якщо В = 0, то пряма паралельна осі у;
якщо С = 0, то пряма проходить через початок координат;
якщо А = 0, С = 0, то пряма збігається з віссю х;
якщо В = 0, С = 0, то пряма збігається з віссю у.
Нагадаємо, що пряма проходить перпендикулярно до вектора 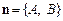 .
.
Геометричним образом лінійного рівняння 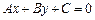 є пряма на площині. Змінні х та у, що входять до рівняння, — це координати множини точок, що лежать на цій прямій. Якщо поділити рівняння прямої на один з відмінних від нуля коефіцієнтів А, В, С, то це рівняння буде залежати від двох параметрів, що визначають розміщення лінії відносно прямокутної системи координат.
є пряма на площині. Змінні х та у, що входять до рівняння, — це координати множини точок, що лежать на цій прямій. Якщо поділити рівняння прямої на один з відмінних від нуля коефіцієнтів А, В, С, то це рівняння буде залежати від двох параметрів, що визначають розміщення лінії відносно прямокутної системи координат.
Наприклад, якщо поділимо на 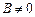 , то одержимо рівняння прямої з кутовим коефіцієнтом:
, то одержимо рівняння прямої з кутовим коефіцієнтом: 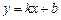 , де
, де 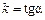 , a — кут нахилу прямої до осі ОХ, b — відрізок, що відтинає пряма на
, a — кут нахилу прямої до осі ОХ, b — відрізок, що відтинає пряма на
осі OY.
Рівняння  , де
, де 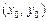 — координати точки, що лежить на прямій, описує множину прямих, що проходять через задану точку.
— координати точки, що лежить на прямій, описує множину прямих, що проходять через задану точку.
Рівняння прямої, що проходить через дві задані точки (х1, у1) та (х2, у2), можна записати у вигляді:
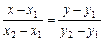 .
.
Якщо рівняння прямої подати у вигляді
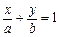 ,
,
то параметри 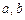 визначають відрізки, що відтинає пряма на відповідних осях системи координат.
визначають відрізки, що відтинає пряма на відповідних осях системи координат.
Кут між двома прямими 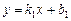 і
і 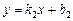 знаходять за формулою:
знаходять за формулою:  , з якої можна одержати умову паралельності (
, з якої можна одержати умову паралельності ( 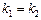 ) і перпендикулярності
) і перпендикулярності 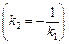 двох прямих. Відстань від точки
двох прямих. Відстань від точки 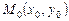 до прямої
до прямої 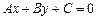 обчислюють за формулою:
обчислюють за формулою:
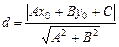 .
.
Приклад 1.Дано рівняння сторін 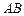
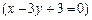 і
і 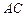
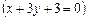 трикутника АВС. Точка
трикутника АВС. Точка 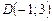 — основа висоти
— основа висоти 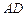 . Записати рівняння медіани АМ, бісектриси AF і висоти AD трикутника, а також знайти кут А.
. Записати рівняння медіани АМ, бісектриси AF і висоти AD трикутника, а також знайти кут А.
Знайдемо координати вершини А. Для цього розв’яжемо си-
стему рівнянь: 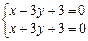 ,
, 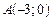 .
.
Запишемо рівняння висоти 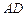 , використовуючи рівняння прямої, що проходить через дві точки
, використовуючи рівняння прямої, що проходить через дві точки 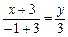 або
або 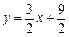 . Використовуючи умову перпендикулярності
. Використовуючи умову перпендикулярності 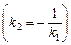 , знайде-
, знайде-
мо кутовий коефіцієнт сторони ВС трикутника:  . Тоді
. Тоді
рівняння сторони ВС можна записати так: 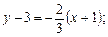 або
або 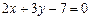 . Знайдемо координати вершин В і С трикутника, розв’язавши відповідно системи рівнянь:
. Знайдемо координати вершин В і С трикутника, розв’язавши відповідно системи рівнянь:
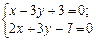 і
і 
Одержимо: 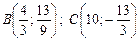 . Основа медіани — це середина відрізка ВС;
. Основа медіани — це середина відрізка ВС; 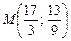 . Використовуючи рівняння прямої, що проходить через дві точки, одержимо рівняння медіани:
. Використовуючи рівняння прямої, що проходить через дві точки, одержимо рівняння медіани: 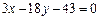 . Знайдемо довжини сторін
. Знайдемо довжини сторін 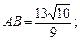
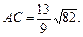 Тоді обчислимо відношення, у якому основа бісектриси поділяє сторону ВС:
Тоді обчислимо відношення, у якому основа бісектриси поділяє сторону ВС: 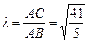 .
.
За формулами 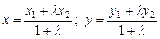 знайдемо координати основи бісектриси
знайдемо координати основи бісектриси 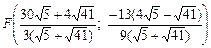 . Рівняння бісектриси запишемо як рівняння прямої, що проходить через задані точки:
. Рівняння бісектриси запишемо як рівняння прямої, що проходить через задані точки: 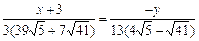 . Для знаходження кута А визначимо кутові коефіцієнти прямої АС —
. Для знаходження кута А визначимо кутові коефіцієнти прямої АС — 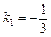 і прямої АВ —
і прямої АВ — 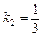 .
.
Тоді 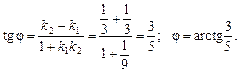
Приклад 2.Дано трикутник 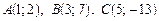 . Знайти відстань від вершини В до медіани, що проходить через точку А.
. Знайти відстань від вершини В до медіани, що проходить через точку А.
Знайдемо координати основи медіани: 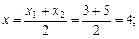
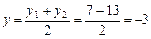 . Запишемо рівняння медіани як прямої, що проходить через дві задані точки:
. Запишемо рівняння медіани як прямої, що проходить через дві задані точки: 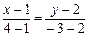 , або
, або 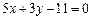 . Відстань від точки
. Відстань від точки 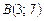 до медіани знайдемо за формулою:
до медіани знайдемо за формулою: 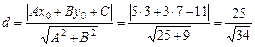 .
.
Приклад 3.Знайти координати точки, що розташована на віддалі 5 одиниць від прямої 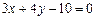 і прямої
і прямої 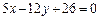 .
.
Нехай 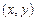 — координати шуканої точки, тоді маємо систему рівнянь:
— координати шуканої точки, тоді маємо систему рівнянь:
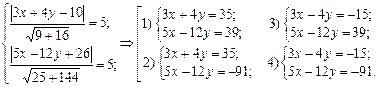
Отже, точок буде чотири: 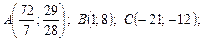
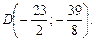
Приклад 4.Скласти рівняння бісектрис кутів, утворених двома прямими 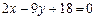 і
і 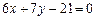 .
.
Бісектриса є множиною точок, рівновіддалених від сторін кута. Нехай 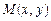 — одна з точок цієї множини. Тоді, прирівнюючи відстані від цієї точки до прямих, маємо:
— одна з точок цієї множини. Тоді, прирівнюючи відстані від цієї точки до прямих, маємо:
 .
.
З останнього рівняння маємо рівняння двох бісектрис у вигляді: 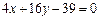 і
і 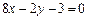 . Слід зазначити, що бісектриси взаємно перпендикулярні:
. Слід зазначити, що бісектриси взаємно перпендикулярні: 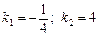 .
.
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,
стор.76 – 80.
Тема 6
Кут між двома прямими. Умови паралельності і перпенди-кулярності прямих. Відстань від точки до прямої
Мета заняття: Навчитися знаходити кут між двома прямими, відстань від точки до прямої, застосовувати умови паралельності та перпендикулярності двох прямих при розв'язуванні задач.
Студенти повинні знати: формули обчислення кута між двома прямими, умови перпендикулярності та паралельності двох прямих; формулу відстані між двома векторами.
Студенти повинні вміти: розв'язувати задачи на обчислення косинуса кута між двома векторами і відстані від точки до прямої; застосовувати умови паралельності і перпендикулярності двох прямих при розв'язуванні задач.
Основні питання теми
1.Знаходження кута між двома прямими (різні види завдання прямої);
2.Умови паралельності двох прямих;
3.Умови перпендикулярності двох прямих;
4.Обчислення відстані від точки до прямої
Завдання для самоперевірки
1.Вивести формулу для знаходження відстані точки від прямої.
2.Знайти кут між прямими х = 4 і 2х – у = 0.
3.Точка А(2;0) є вершиною правильного трикутника, а протилежна сторона лежить на прямій х + у – 1 = 0. Скласти рівняння двох інших сторін.
4.Довести, що пряма 3х + 2у – 6 = 0 перетинає відрізок АВ, де А(1;1) і В(2;2).
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,
стор. 80 – 83.
Лекція ”Кут між прямими”
Розглянемо дві прямі, які задано рівняннями
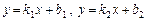 . (1)
. (1)
Якщо прямі паралельні, то вони мають однакові кути нахилу: 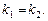
| (2) |
| Дві прямі збігаються, якщо k1 = k2, b1 = b2. |
Якщо прямі взаємно перпендикулярні, то 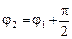 і
і
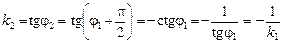 .
.
Рівність
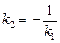 є умовою перпендикулярності двох прямих виду (1).
є умовою перпендикулярності двох прямих виду (1).
| (3) |
Якщо прямі не паралельні, то вони перетинаються в точці М(х, у), координати якої є розв’язком системи рівнянь
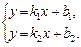
Нехай q — кут між цими прямими (мал. 1).
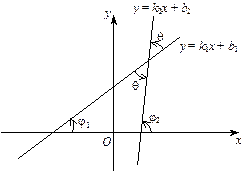
Мал. 1
Згідно з рис. 1 маємо: j2 = j1 + q (зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних з ним). Отже,
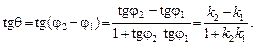
Формулу
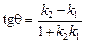 застосовують для знаходження кута між двома прямими, заданими рівняннями виду (1).
застосовують для знаходження кута між двома прямими, заданими рівняннями виду (1).
| (4) |
Приклад. У трикутнику з вершинами А(1, 1), В(5, 1), С(2, 4) знайти кут a при вершині А, а також рівняння висоти CD і медіани ВМ (мал. 2).
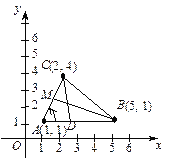
мал. 2
Скориставшись (3), знайдемо кутові коефіцієнти прямих АВ, АС:
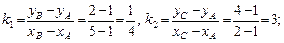
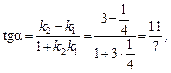
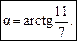
Пряма СD перпендикулярна до прямої АВ. Її кутовий коефіцієнт 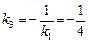 , а відповідне рівняння
, а відповідне рівняння
у – 4 = – 4(х – 2).
Точка М поділяє відрізок АС пополам. Отже,
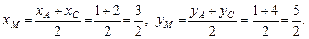
Через точки В(5, 2), М 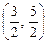 проводимо пряму m і згідно з (4) дістаємо:
проводимо пряму m і згідно з (4) дістаємо:
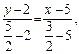 або
або 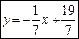 . ·
. ·
Взаємне розташування двох прямих
Дві прямі задано їх загальними рівняннями:
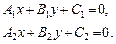 (1)
(1)
Точку перетину М(х, у) цих прямих знаходимо, розв’язуючи систему рівнянь (1), оскільки координати х, у точки М задовольняють одночасно обидва ці рівняння.
Кут q між даними прямими дорівнює куту між їх нормалями 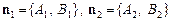 (мал. 3).
(мал. 3).
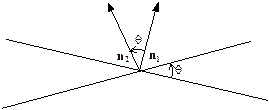
мал. 3
Отже, маємо такі залежності:
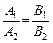 — умова паралельності прямих. — умова паралельності прямих.
| (2) |
Якщо прямі збігаються, то їх коефіцієнти пропорційні:
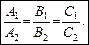
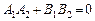 — умова перпендикулярності прямих. — умова перпендикулярності прямих.
| (3) |
Скориставшись формулою скалярного добутку векторів, знайдемо кут q:
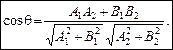 (4)
(4)
Розглянемо спосіб побудови прямих, що проходять через точку перетину двох даних прямих.
Теорема 1. Якщо прямі (1) не паралельні, то рівняння
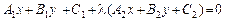 (5)
(5)
| <== попередня сторінка | | | наступна сторінка ==> |
| Розглянемо систему однорідних рівнянь | | | Визначає пучок прямих, які проходять через точку перетину прямих (1). Вибором l можна дістати будь-яку пряму, що проходить через точку перетину прямих (1), крім другої прямої. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |