• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Площина і пряма у просторі

Будь-яке рівняння першого степеня відносно координат точки простору 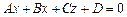відображає площину. Коефіцієнти при змінних А, В, С є компонентами вектора, перпендикулярного до площини.

Кут між двома площинами 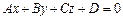і 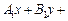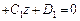визначається за формулою:

.

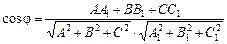Умовою їх паралельності є: 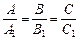, а перпендикулярності — 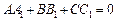. Відстань від точки 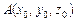до площини можна знайти за формулою: .

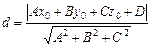Пряма у просторі може бути визначена як перетин двох
площин:

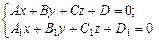
або канонічним рівнянням:

,

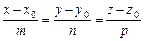де — напрямний вектор прямої, 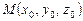— точка, що лежить на прямій.

Пряму у просторі можна задати також параметричним рівнянням:

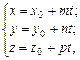
де t — параметр, або рівнянням прямої, що проходить через дві задані точки 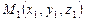і :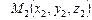

.

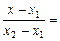
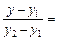
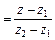Звичайно, всі рівняння відповідають прямій у просторі і між ними існує певний зв’язок.

Площина і пряма у просторі можуть перетинатися під деяким кутом a, який визначається за формулою:

.

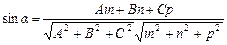У разі виконання умови: 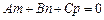пряма і площина па-
ралельні, а якщо 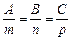— перпендикулярні. Умовою того, що пряма лежить на площині, є виконання співвідношень:

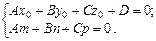
Приклад 1.Скласти рівняння площини, що проходитьчерез вісь ОZ і утворює з площиною 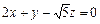кут 60°, і знаходження її відстані до точки .

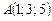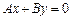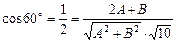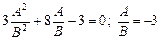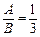Рівняння шуканої площини можна записати у вигляді , тому що вона проходить через вісь OZ. Використаємо другу умову задачі: , з якої одержимо рівняння: або . Остаточно маємо, що умовам задачі задовольняють дві площини: 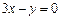і 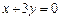. Точка А лежить на першій площині, тому що 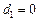, а відстань її до другої площини .

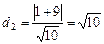Приклад 2.Знайти напрямний вектор прямої

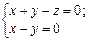
і кути, які вона утворює з осями системи координат.

Вектори 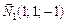і 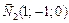перпендикулярні до відповідних площин, що задають рівняння прямої, тому напрямний вектор прямої 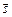розташований перпендикулярно до кожного з векторів 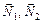. Згідно з означенням векторного добутку векторів

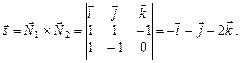
Тобто: або 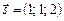. Кути з осями знайдемо за формулами: ; .

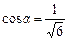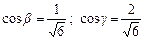Приклад 3.Показати, що прям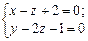і

і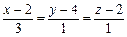

перетинаються, і написати рівняння площини, в якій вони роз-
ташовані.

Дві прямі будуть лежати на одній площині, коли їх напрямні вектори 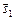і і вектор 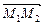будуть компланарними. Точка 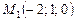лежить на першій прямій, а 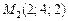— на другій. Век­тор 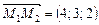. Напрямний вектор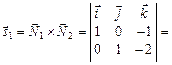
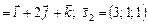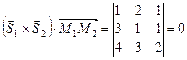. . Отже, прямі лежать на одній площині. Для запису рівняння цієї площини знайдемо вектор 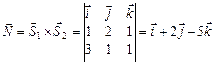. Точка 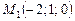лежить на цій площині. Отже, маємо: 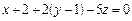або остаточно: .

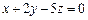Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,

стор. 90 – 96.

Тема 9

Гіпербола. Парабола. Властивості

Мета заняття Вивчити означення, виведення канонічного рівняння та властивості кривих: гіпербола та парабола.

Розвивати логічне мислення.

Студенти повинні знати: означення гіперболи, її рівняння, властивості; означення параболи, її рівняння, властивості.

Студенти повинні вміти: розв'язувати задачі, складати різні рівняня гіперболи; розв'язувати задачі, складати різні рівняння параболи; будувати ці криві в системі координат залежно від їх рівняння.

Основні питання теми

1.Означення гіперболи;

2.Розташування в системі координат;

3.Виведення канонічного рівняння;

4.Властивості: осі, вершини, фокуси, асимптоти, ексцентриситет, загальне рівняння, спряжені гіперболи, рівнобічна гіпербола;

5.Означення параболи;

6.Виведення канонічного рівняння параболи;

7.Властивості: вершина, фокус, директриса, вісь симетрії;

8.Розташування параболи в системі координат залежно від її рівняння;

2.5. Криві другого порядку

До кривих другого порядку належать: коло, еліпс, гіпербола, парабола. У загальному випадку їм відповідає рівняння:

.

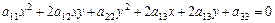Шляхом перетворення системи координат із загального рівняння можна одержати канонічні рівняння кривих другого порядку:

кола: 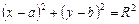, де 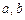— координати центра кола,
а 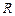— радіус кола;

еліпса: 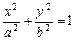, де 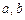— півосі еліпса;

гіперболи: 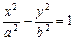, де а — дійсна, b — уявна півосі гіперболи;

параболи: , де р — параметр параболи.

Переглядів: 4233