
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Множини та операції над ними
ПЕРЕДМОВА
Дискретна математика є розділом математики, що зародилася в давні часи. Її головною відмінністю є дискретність, тобто антипод неперервності. Дискретна математика включає в себе як традиційні розділи, які вже сформувалися (теорію множин, математичну логіку, комбінаторику, теорію графів та ін.), так і нові, що інтенсивно розвиваються (теорію алгоритмів, кодування та ін.).
Спеціалісти, які займаються прикладними дослідженнями, програмуванням мають все більшу потребу у використанні апарату дискретної математики, що пояснюється широким застосуванням комп’ютерної техніки та інформаційних технологій. Тому сьогодні дисципліна “Дискретна математика” є однією з основних фундаментальних дисциплін у загальнонауковій підготовці студентів – комп’ютерників.
Методичні рекомендації мають за мету надання допомоги студентам у організації їх самостійної роботи з опанування курсу дисципліни. Зміст і стиль подання матеріалу у посібнику повністю відповідає навчальній програмі дисципліни “Дискретна математика” та задовольняє потреби суміжних математичних і прикладних дисциплін.
Самостійна робота студентів передбачає поглиблене вивчення тем, що розглядаються на лекціях та виконання графічно-розрахункової роботи. Виконання практичних завдань є необхідною умовою засвоєння теоретичного курсу, а також істотною складовою самостійної роботи студентів – запоруки успішного оволодіння курсом дискретної математики.
Для зручності цей посібник в кожному розділі містить стислий довідковий матеріал (означення, формули та ін.). Наведені приклади розв’язання деяких типових задач. Слід відмітити, що розв’язуванню практичних завдань повинно передувати вивчення теоретичного матеріалу на лекційних аудиторних заняттях, а також шляхом самостійного опрацювання з використанням рекомендованої літератури.
| № п/п | Вид самостійної роботи | |
| Найменування тем, що винесені на самостійне вивчення | Рекомендована література | |
| Теорія множин | Л1 (ст. 16-30) | |
| Відношення | Л1 (ст. 99-125) |
Множини та операції над ними
Під множиноюзазвичай розуміють об’єднання в одне ціле об’єктів, що добре розрізняються нашою думкою або інтуїцією.
Об’єкти, що утворюють множину, називаються елементамимножини. Елементи звичайно позначаються малими літерами латинського алфавіту, а множини великими. Якщо m є елемент, який належить множині М, то використовується запис 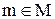 , у протилежному випадку -
, у протилежному випадку - 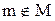 . Читається так: m належить М.
. Читається так: m належить М.
Означення. Множина, яка містить скінченне число елементів, називається скінченною, а множина, що містить нескінченне число елементів, - нескінченною.
Множина може задаватися різними способами: перерахуваннямелементів для скінченної множини або зазначенням їх властивостей. У разі перерахування використовують фігурні дужки {}. Наприклад, множину М цифр десяткового алфавіту можна задати у вигляді М={0, 1, …, 9}.
Цю ж саму множину можна задати й інакше, як М={i|i – ціле, 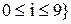 }, де справа від вертикальної риски зазначається характеристична властивість елементів цієї множини.
}, де справа від вертикальної риски зазначається характеристична властивість елементів цієї множини.
Якщо ж множина М є множиною, наприклад, парних чисел, то вона записується як М={m|m – парне число} або М={m|m=2k, kÎN}.
Іноді нескінченні множини задаються простим перерахуванням кількох перших елементів, і тоді характеристична властивість є заданою в неявному вигляді. Наприклад, множину парних чисел можна задати у вигляді A={2,4,6,8,…}.
Для того, щоб позначити множину всіх предметів, що є елементами множини А і мають властивість P, замість {x| 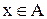 i P(x)} часто пишуть {
i P(x)} часто пишуть { 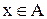 |P(x)}.
|P(x)}.
Наприклад, 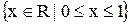 означає множину всіх дійсних чисел від 0 та 1 включно, а
означає множину всіх дійсних чисел від 0 та 1 включно, а  - множину всіх додатних раціональних чисел, квадрати яких менші за число 2.
- множину всіх додатних раціональних чисел, квадрати яких менші за число 2.
Множина М’ називається підмножиною множини М тоді й лише тоді, коли будь-який елемент множини М’ і М можуть збігатись, якщо М’ може дорівнювати М, то тоді пишуть, що 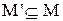 , де
, де 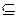 - знак включення підмножини. Невключення підмножини М’ до множини М позначається як
- знак включення підмножини. Невключення підмножини М’ до множини М позначається як  .
.
Множина А, що строго включається до В, позначається як 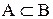 . Це означає, що В містить і інші елементи, крім елементів А, і це особливо підкреслюється.
. Це означає, що В містить і інші елементи, крім елементів А, і це особливо підкреслюється.
Дві множини рівні тільки тоді, коли вони складаються з одних і тих самих елементів. Тому будь-яка множина Х=Х.
Рівність двох множин Х і Y позначається через Х=Y, а нерівність множин Х і Y – через Х ≠ Y. Для будь-яких рівних множин Х, Y і Х, Y, Z виконуються умови:
1. Якщо Х=Y, то Y=X;
2. Якщо Х=Y та Y=Z, то Х=Z.
Порядок елементів у множині не є суттєвим. Множини {3,4,5,6} і {4,5,6,3} являють собою одну й ту саму множину.
Множини не містять однакових елементів. Так, множина простих дільників числа 60 дорівнює {2,3,5}, а не {2,2,3,5}.
Слід розрізняти об’єкт і множину, єдиним елементом якої є цей об’єкт. Так множина {1,2} становить об’єкт, який є елементом множини {{1,2}}. Множини {{1,2}} і {1,2} не рівні, оскільки перша – одноелементна множина, що має єдиний елемент {1,2} , а друга має два елементи 1 і 2.
Якщо множина не містить жодного елемента, то вона називається порожньою і позначається 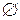 . Інколи її називають ще пустоюмножиною. Наприклад, множина трикутників з двома прямими кутами є порожньою. Також множина простих чисел, які діляться на число чотири, є порожньою. Але множина {
. Інколи її називають ще пустоюмножиною. Наприклад, множина трикутників з двома прямими кутами є порожньою. Також множина простих чисел, які діляться на число чотири, є порожньою. Але множина { 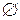 } не є порожньою, тобто
} не є порожньою, тобто 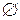 ={
={ 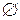 }; ця множина є одноелементною. Її єдиним елементом є порожня множина.
}; ця множина є одноелементною. Її єдиним елементом є порожня множина.
Усі підмножини множини А, яка складаються з n елементів, створюють множину, що називається множиною-степенем, або булеаном множини А і позначається Р(А) або В(А). Якщо, наприклад, А={1,2,3}, то множина-степінь
Р(А)={ {1,2,3},{1,2,},{1,3},{2,3},{1},{2},{3},{  }}. (1.1)
}}. (1.1)
Теорема. Множина-степінь Р(А) множини 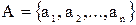 має
має 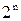 різних підмножин.
різних підмножин.
Приклад 1.Чи є множини {2,4,6} , {2,6,4} рівними?
Оскільки множини {2,4,6} і {2,6,4} складаються з одних і тих самих елементів, то вони будуть рівними.
Приклад 2.Чи є множини {{1,2},{2,3}}, {1,2,3} і {1,2,{3}} рівними?
Ні, не будуть, оскільки елементами першої множини будуть елементи {1,2} і {2,3}, другої – 1,2,3 і третьої – 1, 2, {3}.
Приклад 3.Чи є множини {{1,2}} і {1,2} рівними?
Ні, не є рівними, оскільки перша – одноелементна множина, що має своїм єдиним елементом {1,2} , а друга має своїми елементами 1 і 2.
Приклад 4.Чи правильно, що {1,2} 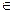 {{1,2,3},{1,3},1,2}?
{{1,2,3},{1,3},1,2}?
Ні, не правильно, оскільки в правій множині відсутній елемент {1,2}.
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Операції над множинами |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |