Функції на множинах (відображення)

Математичне поняття функції виражає інтуїтивне уявлення про те, як одна величина повністю визначає значення іншої величини. Так, значення змінної x однозначно визначає значення виразу 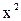, а значення місяця однозначно визначає значення наступного за ним місяця. Аналогічно, деякий задуманий наперед алгоритм за варійованими вхідними даними видає певні вихідні значення. Зазвичай розглядають числові функції, які ставлять одні числа у відповідність іншим. Такі функції володіють низкою відмінностей і зручно представляються на рисунках у вигляді графіків.

Існують два визначення функцій.

1) інтуїтивне - поняття функції перекладається звичайною мовою, при цьому використовуючи слова «закон», «правило» або «відповідність».

Означення. Функція f(відображення, операція, оператор) – це закон або правило, згідно якому кожному елементу x з множини Xставиться у відповідність єдиний елемент у з множини Y.

При цьому говорять, що функція f заданана множині X, або що f відображує X в Y.

Якщо елементу 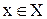відповідає елемент 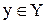, то говорять, що елемент у знаходиться у функціональній залежності f від елементу x. При цьому змінна x називається аргументом функції f або незалежною змінною.

Множина X називається областю задання або областю визначення функції, а елемент у, відповідний конкретному елементу x, – значенням функції f в точці x.

Множина Y всіх можливих значень функції f називається її областю значень або областю зміни.

2) теоретико-множинне - визначення на основі поняття бінарного відношення, яке є більш суворішим.

У теоретично-множинному визначенні функцію f зручно подати як бінарне відношення (тобто множина впорядкованих пар 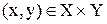), яке задовольняє наступній умові: для будь-якого 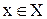існує єдиний елемент 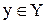такий, що .

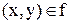Розглянемо дві множини Х та Y.

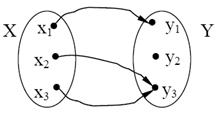
Рисунок 1.7. Відображення множини Х у множину Y

Означення. Якщо кожному елементу 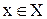відповідає єдиний елемент 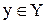, то така відповідність називається відображенням множини Х у множину Y(рис. 1.7).

Позначення: f: X→Y, f – символ самого відображення.

Означення. Якщо при відображенні f кожний елемент множини Y є образом хоча б одного елементу з множини Х, то f називають сюр’єнктивною функцією або сюр’єнцією(рис. 1.8).

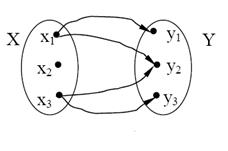
Рисунок 1.8. Ілюстрація відображення сюр’єнції

Приклад. Нехай Х – множина студентів, Y – множина книг. Відображення «студенту х належить книга у» задає сюр’єнцію, оскільки будь-яка книга може належати одному або декільком студентам, а деякі студенти книг взагалі не мають.

Означення. Якщо при відображенні f всі різні елементи множини Х переходять в різні елементи множини Y, то відображення f називають ін’єнктивною функцієюабо ін’єнцією(рис. 1.9).

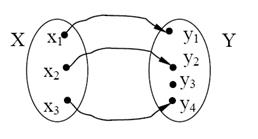
Рисунок 1.9. Ілюстрація відображення ін’єнції

Приклад. Нехай Х – множина студентів, Y – множина стільців в аудиторії. Відображення «студент х сидить на стільці у» задає ін’єнцію, оскільки кожний студент сидить на стільці, але в аудиторії є ще й вільні стільці.

Означення. Якщо при відображенні f кожному елементу 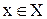відповідає один елемент 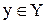, при чому кожному елементу 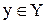відповідає єдиний елемент 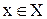, то відображення f називається взаємно однозначною функцією(рис. 1.10).

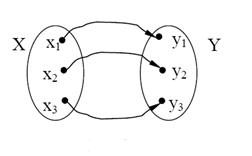
Рисунок 1.10. Ілюстрація взаємно однозначного відображення

Приклад. Нехай Х – множина студентів, Y – множина залікових книжок. Відображення «студенту х належить залікова книжка у» є взаємно однозначним, оскільки певному студенту належить відповідно одна його залікова книжка і навпаки.

<== попередня сторінка	\|	наступна сторінка ==>
Властивості множин	\|	Бінарні відношення

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.007 сек.