• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Частотні характеристики реактивних двополюсників.

Розглянемо частотну характеристику (ЧХ) вхідного опору реактивного двополюсникавід частоти (Z=f(w). При конструюванні кола, яке складається із котушок індуктивностей і конденсаторів, наприклад LC-фільтрів та фазо-обертаючих контурів, для виявлення особливостей частотної характеристики часто можна знехтувати малими активними складовими, тобто вважати двопо-люсник чисто реактивним, отже вхідний опір буде чисто реактивний Х = Х(w).

Частотні характеристики таких двополюсників мають визначені законо-мірності, які дозволяють просто синтезувати двополюсник за заданою ЧХ.

Найпростіші реактивні двополюсники – це індуктивність і ємність С, комплексні опори яких : .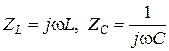

Визначення ЧХ реактивних двополюсників показано на прикладах.

1. Послідовне з’єднання реактивних опорів (Рис. 40).

Вхідний опір кола: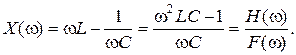

Чисельник Н(w) і знаменник Н(w) функції частоти. Вхідний опір – дріб, дорівнює нулю, коли нулю дорівнює чисельник (нуль функції). Коли ж нулю дорівнює знаменник, вхідний опір дорівнює нескінченості – полюс функції.

Визначення нулів та полюсів функції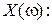

звідки: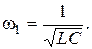

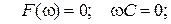звідки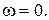

Вхідний опір дорівнює нескінченості (розрив) при нульовій частоті (пос-тійний струм через конденсатор не проходить), а при резонасній частоті 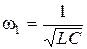, коли реактивні опори однакові, вхідний опір дорівнює нулю.

Схематично частотна характеристика показана на Рис. 41.

2. Паралельне з’єднання реактивних опорів (Рис. 42).

Вхідний опір кола:

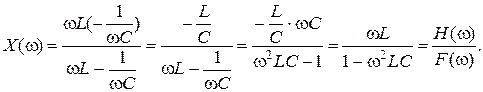
Визначення нулів та полюсів функції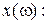

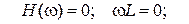звідки: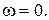

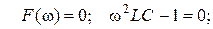звідки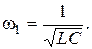

При нульовій частоті вхідний опір дорівнює нулю (постійний струм замика-ється по індуктивності (к.з). При частоті 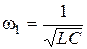у колі спостерігається резонанс струмів, вхідний опір при цьому дорівнює нескінечності.

Схематично частотна характеристика показана на Рис. 43.

2. Змішане з’єднання реактивних опорів (Рис. 44).

Вхідний опір кола:

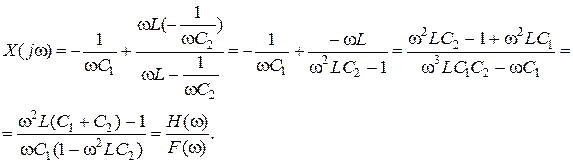
Визначення нулів та полюсів функції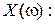

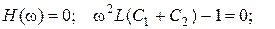звідки: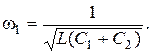

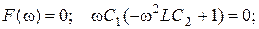звідки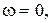

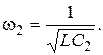
При нульовій частоті 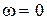і частоті 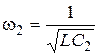вхідний опір дорівнює нескінченості (полюс функції) – паралельний резонанс (резонанс струмів) , а при частоті 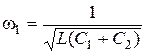дорівнює нулю (нуль функції) – послідовний резонанс (резонанс напруг). Схематично частотна характеристика показана на Рис. 45.

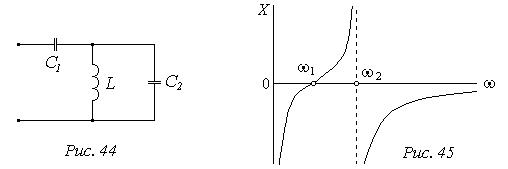
Спільною рисою всіх розглянутих характеристик є виконання умови 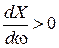, звідки можна зробити висновок, що нулі і полюси чергуються, тобто, якщо перший був нуль, за ним обов’язково буде полюс. Для всіх реактивних двополюсників із послідовно-паралельних віток можна по вигляду схеми знай-ти число частот послідовного і паралельного резонансів.

Будемо вважати, що послідовне чи паралельне з’єднання однотипних еле-ментів (L, С) замінено еквівалентними елементами. Тоді двополюсник із двох елементів (L, С) має одну резонансну частоту (Рис. 41, Рис. 43). Ускладнення схеми на один елемент збільшує число резонансних частот на одну (Рис . 45)

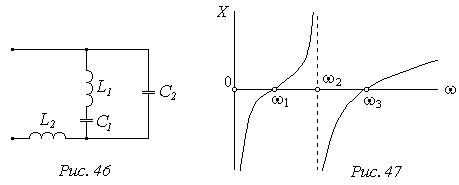
У двополюсника Рис. 46, два нулі і два полюси при 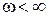. Прямого шляху через індуктивність для постійного струму немає, відповідно, при 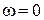частотна характеристика починається зі значення 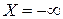(полюс), а перша із резонансних частот w₁ - частота послідовного резонансу (нуль) (Рис. 47), далі чергуються полюс w₂ і нуль w₃. Загальна кількість нулів і полюсів частотної характеристики 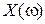дорівнює кількості незалежних реактивних елементів плюс один нуль або полюс при .

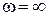Приклад 5.

А) Побудувати частотну характеристику для реактивного двополюсника, показаного на Рис. П5.1 Він утворений з двополюсника (Рис. П1), в якому всі активні опори дорівнюють нулю. Параметри реактивних елементів знаходяться з умови, що у Прикладі 1 індуктивні і ємнісні опори задані для частоти 50 (Гц).

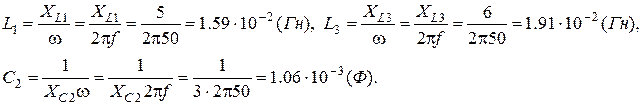
По схемі можна визначити, що частотна характеристика почнеться з нуля (є прямий шлях через індуктивності для постійного струму 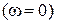, потім буде перша резонансна частота струмів w₁ (полюс),за ним друга резонансна частота напруг w₂ (нуль). Вхідний опір двополюсника:

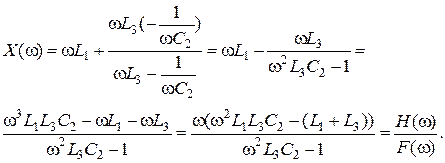
Визначення нулів та полюсів функції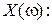

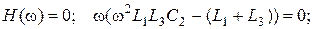звідки: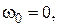

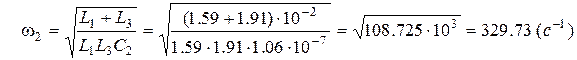
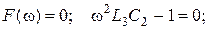звідки

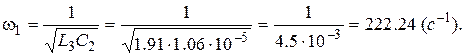
Підставляючи значення частоти w від 0 до 400 (с^-1) у рівняння вхідного опору будуємо частотну характеристику реактивного двополюсникапоказануна Рис. П5.2.

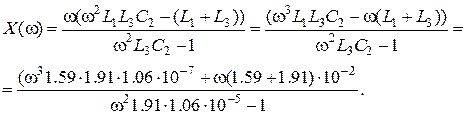
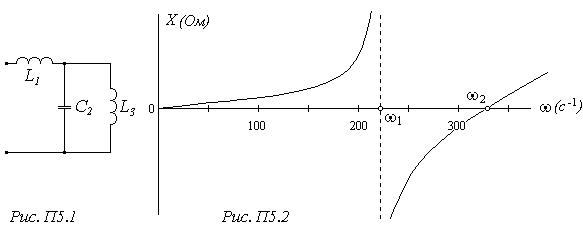
Аналогічно розраховується частотна характеристика для більш складних схем, при цьому степінь рівнянь у чисельнику та знаменнику відповідно збільшується з кількістю елементів у вітках схеми.

Б) Побудувати частотну характеристику для реактивного двополюсника, показаного на Рис. П5.3 . Параметри реактивних елементів:

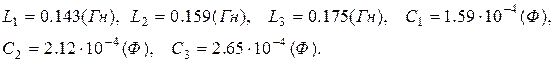
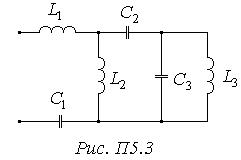
По схемі можна визначити, що частотна характеристика почнеться з полюса (немає прямого шляху через індуктивнісь для постійного струму при 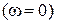) і закінчиться полюсом (немає прямого шляху через ємність при ( )).

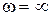Вхідний опір двополюсника знаходиться послідовним та паралельним складанням елементів схеми.

1.

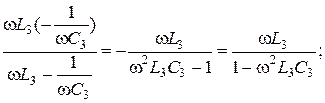
2.

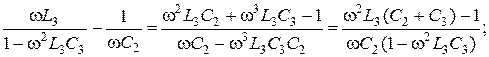
3.

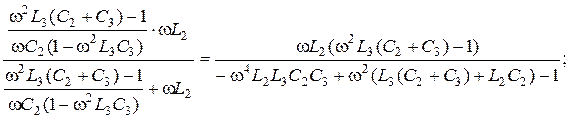
4.

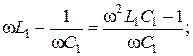
5.

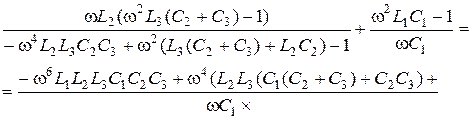
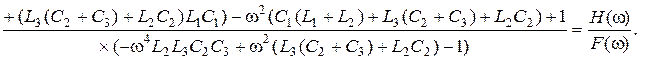
Підставляєм дані параметрів:

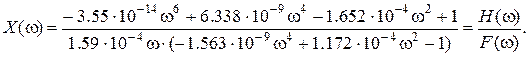
Визначення нулів та полюсів функції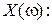

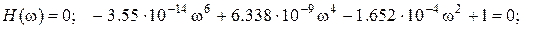
Для зниження степені рівняння приймаємо:t = w², тоді:

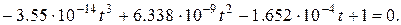
Розв’язок кубічного рівняння дає корені:

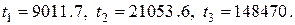
Звідки значення частот нулів частотної характеристики:

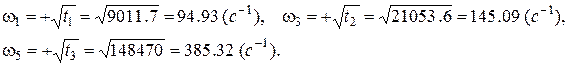
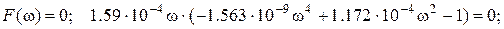
звідки: 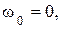а за коренями біквадратного рівняння (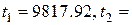

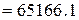) визначаємо значення частот полюсів частотної характеристики:

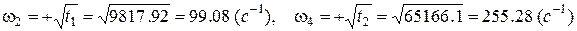
Підставляючи значення частоти w від 0 до 400 (с^-1) у рівняння вхідного опору будуємо частотну характеристику реактивного двополюсника Рис. П5.4.

Переглядів: 1993