
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Розв’язування.
Розглянемо рух механічної системи, що складається з тіл 1, 2, 3, 4, з’єднаних нитками. Система має одну ступінь вільності. В’язі, накладені на систему, є ідеальними.
Для визначення прискорення вантажу 3 – 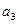 використаємо загальне рівняння динаміки:
використаємо загальне рівняння динаміки:
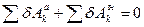 , (5.1)
, (5.1)
де 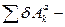 сума можливих робіт активних сил, що діють на систему;
сума можливих робіт активних сил, що діють на систему; 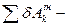 сума можливих робіт сил інерції.
сума можливих робіт сил інерції.
Зобразимо діючі на систему активні сили 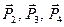 і пару сил з моментом
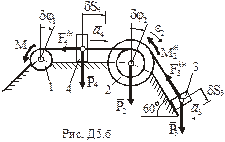
і пару сил з моментом  (рис.Д5.б). Задамо напрям прискорень тіл. Прикладемо сили інерції тіл 3 і 4 (
(рис.Д5.б). Задамо напрям прискорень тіл. Прикладемо сили інерції тіл 3 і 4 ( 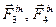 ), які виконують поступальний рух. Зобразимо момент сил інерції тіла 2 (
), які виконують поступальний рух. Зобразимо момент сил інерції тіла 2 ( 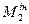 ), яке обертається навколо нерухомої осі. Напрямок інерційних сил і моментів - протилежно відповідним прискоренням.
), яке обертається навколо нерухомої осі. Напрямок інерційних сил і моментів - протилежно відповідним прискоренням.
 Чисельно вони дорівнюють:
Чисельно вони дорівнюють:
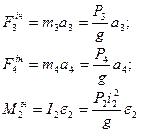 (5.2)
(5.2)
Задамо системі (рис. Д5.б) можливе переміщення та складемо загальне рівняння динаміки для системи:
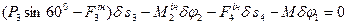 (5.3)
(5.3)
Через те, що механічна система має один ступінь вільності, виразимо всі можливі переміщення через одне, наприклад, 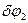 :
:
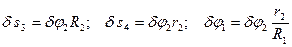 (5.4)
(5.4)
Підставимо величини (5.2) та (5.4) в рівняння (5.3) і отримаємо:
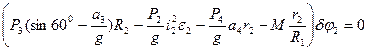 (5.5)
(5.5)
Всі прискорення, що входять до (5.5), виразимо через шукане 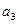 :
:
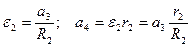 (5.6)
(5.6)
Враховуючи, що можливі переміщення нескінченно малі, але не дорівнюють нулю ( тобто 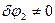 ) , та враховуючи (5.6) отримаємо:
) , та враховуючи (5.6) отримаємо:
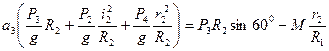 (5.7)
(5.7)
Приймемо 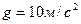 , підставимо числові значення та знайдемо
, підставимо числові значення та знайдемо 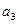 :
: 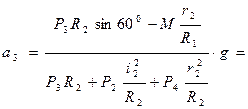
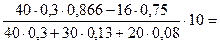
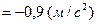
|
Відповідь:
Завдання Д-6. Рівняння Лагранжа II роду
Умова завдання. Механічна система складається із ступінчастих шківів 1 і 2 вагою 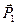 і
і 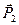 з радіусами ступіней
з радіусами ступіней 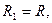
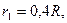
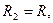
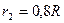 (масу кожного шківа вважати рівномірно розподіленою на зовнішньому ободі); вантажів 3, 4 та однорідного циліндричного котка 5 вагою
(масу кожного шківа вважати рівномірно розподіленою на зовнішньому ободі); вантажів 3, 4 та однорідного циліндричного котка 5 вагою 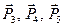 відповідно (рис. Д6.0 – Д6.9, табл. Д6). Тіла з’єднані нерозтяжними нитками, намотаними на шківи; нитки паралельні відповідним площинам. Вантажі рухаються без тертя; коток котиться без ковзання.
відповідно (рис. Д6.0 – Д6.9, табл. Д6). Тіла з’єднані нерозтяжними нитками, намотаними на шківи; нитки паралельні відповідним площинам. Вантажі рухаються без тертя; коток котиться без ковзання.
Система рухається під дією постійної сили 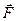 ; на шківи 1 і 2 діють моменти сил опору, що дорівнюють відповідно
; на шківи 1 і 2 діють моменти сил опору, що дорівнюють відповідно 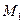 і
і 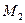 .
.
Вантажі, вага яких дорівнює нулю, на рисунку не зображати, шківи 1 і 2 завжди входять в систему. При обчисленні кутового прискорення  або
або 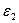 вважати
вважати 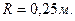
Визначити: параметри, зазначені у стовпці „Знайти”.
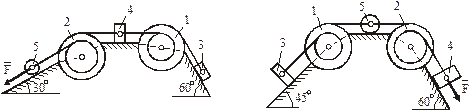 |
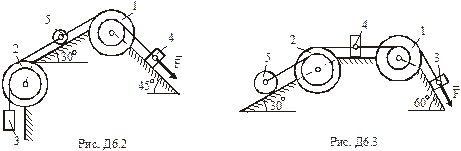
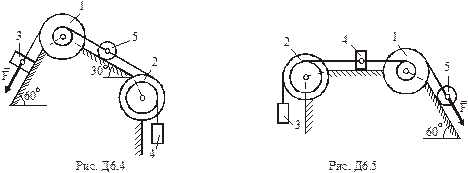
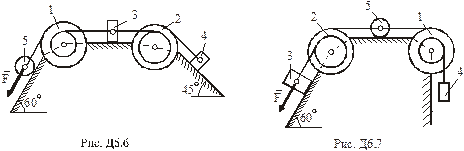
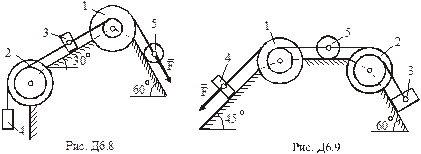
Табл.Д6
| № умови | 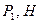
| 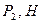
| 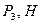
| 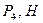
| 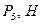
| 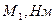
| 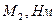
| 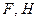
| Знайти |
| 12Р 10Р 8Р 12Р 10Р 12Р | 10Р 12P 10P 12P 8P 12P | P 2P 2P 2P | 4P 2P 3p 5P | 3P 2P P 3P 2P P 4P 2P 4P 3P | 0,2PR 0,3PR 0,2PR 0,3PR 0,2PR | 0,3PR 0,2PR 0,3PR 0,4PR 0,2PR | 8P 6P 4P 10P 5P 8P 6P 5P 6P 10P | a3 e2 e1 a3 aC5 e1 a4 e2 a4 aC5 |
Теоретичне обґрунтування : [5] § 142 – 146 ; [6] Розд.III. Гл.6. § 5 – 7 , 9;
[7] § 112, 119, 125, 128 ; [8]; [9]; [11]; [12]; [13].
Методичні вказівки. Завдання Д-6 на тему “Рівняння Лагранжа II роду”. Рівняння Лагранжа II роду мають вигляд:
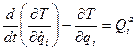 , (Д6.1)
, (Д6.1)
де 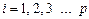 (
( 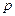 - кількість ступенів вільності системи);
- кількість ступенів вільності системи);
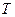 - кінетична енергія системи;
- кінетична енергія системи;
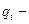 і-та узагальнена координата;
і-та узагальнена координата;
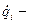 і-та узагальнена швидкість;
і-та узагальнена швидкість;
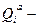 узагальнена активна сила, що відповідає і–ій узагальненій координаті (при розв’язуванні конкретних задач зручно позначати через
узагальнена активна сила, що відповідає і–ій узагальненій координаті (при розв’язуванні конкретних задач зручно позначати через 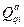 ).
).
Кількість рівнянь Лагранжа II роду, що складається для розв’язування задачі, повинна дорівнювати кількості ступенів вільності, тобто кількості незалежних можливих переміщень, що має система.
Узагальнена активна сила визначається за формулою:
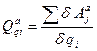 , (Д6.2)
, (Д6.2)
де 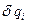 - можливе зростання узагальненої координати (
- можливе зростання узагальненої координати ( 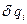 >0);
>0);
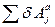 - сума можливих робіт активних сил, що відбувається на можливому переміщені системи за умовою, що
- сума можливих робіт активних сил, що відбувається на можливому переміщені системи за умовою, що 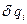 >0;
>0;
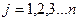 (
( 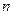 - кількість активних сил, що діють на систему).
- кількість активних сил, що діють на систему).
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклад Д-5 | | | Приклад Д-6 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |
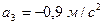 . Знак “-“ указує на те, що прискорення вантажу 3 та прискорення інших тіл системи спрямовані протилежно показаним на рис. Д5.б.
. Знак “-“ указує на те, що прискорення вантажу 3 та прискорення інших тіл системи спрямовані протилежно показаним на рис. Д5.б.