
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Постановка задачі. Симплекс-метод.
Лабораторна робота №2
«Дослідження симплекс-методу»
Мета: Ознайомитися з задачею лінійного програмування в загальному вигляді, навчитися складати базисний план, симплексні таблиці та здійснювати заміну базисних змінних, вивчити алгоритм симплекс методу та застосувати його для розв’язання ЗЛП.
Постановка задачі. Симплекс-метод.
Лінійне програмування – це наука про методи дослідження та пошуку найбільших та найменших значень лінійної функції, на невідомі якої накладені лінійні обмеження. Таким чином, задачі лінійного програмування відносяться до задач на умовний екстремум функції.
Канонічна форма задачі лінійного програмування:
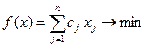 (1)
(1)
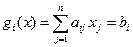 ,
, 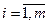 (2)
(2)
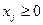 ;
;  (3)
(3)
(1) - цільова лінійна функція;
(2) і (3) –обмеження у вигляді лінійних рівнянь та нерівностей.
Необхідно знайти вектор значень змінних х, який перетворює в оптимум (1) при дотриманні обмежень (2) і (3).
Для розв’язання задачі лінійного програмування, кількість вільних змінних в якій n – m >= 3, геометрична інтерпретація, якою користувалися раніше, є недоцільною.
Оптимальний розв’язок задачі лінійного програмування пов’язаний з кутовими точками багатокутника рішень. Існує така кутова точка багатокутника рішень, в якій лінійна функція досягає свого найменшого (найбільшого) значення. Кожній кутовій точці багатокутника рішень відповідає базисний план. Кожен базисний план визначається системою m лінійно незалежних векторів, що містяться в даній системі з n векторів, 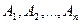 . Для відшукання оптимального плану необхідно дослідити лише базисні плани. Верхня межа кількості базисних планів, що міститься в даній задачі, визначається числом сполучень
. Для відшукання оптимального плану необхідно дослідити лише базисні плани. Верхня межа кількості базисних планів, що міститься в даній задачі, визначається числом сполучень 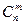 . При більших m і n знайти оптимальний план, перебираючи всі базисні плани задачі, дуже важко. Тому необхідно мати схему, що дозволяє здійснити впорядкований перехід від одного базисного плану до іншого. Такою схемою є симплекс-метод, який дозволяє, виходячи з відомого базисного плану, за кінцеве число кроків отримати її оптимальний план. Кожен з кроків (ітерацій) полягає в знаходженні нового плану, якому відповідає менше значення лінійної функції, ніж значення цієї ж функції в попередньому плані. Процес продовжують до отримання оптимального плану. Якщо задача не має планів або її лінійна функція не обмежена на багатокутнику рішень, то симплексний метод дозволяє встановити це в процесі розв’язування.
. При більших m і n знайти оптимальний план, перебираючи всі базисні плани задачі, дуже важко. Тому необхідно мати схему, що дозволяє здійснити впорядкований перехід від одного базисного плану до іншого. Такою схемою є симплекс-метод, який дозволяє, виходячи з відомого базисного плану, за кінцеве число кроків отримати її оптимальний план. Кожен з кроків (ітерацій) полягає в знаходженні нового плану, якому відповідає менше значення лінійної функції, ніж значення цієї ж функції в попередньому плані. Процес продовжують до отримання оптимального плану. Якщо задача не має планів або її лінійна функція не обмежена на багатокутнику рішень, то симплексний метод дозволяє встановити це в процесі розв’язування.
Функція, яку необхідно оптимізувати, в загальному випадку має наступний вигляд:
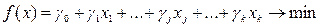 (1)
(1)
Для цільової лінійної функції існує ряд обмежень (2):
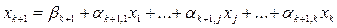
………………………………………..
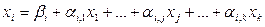
……………………………………
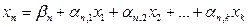 ;
;
 ;
; 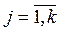 .
.
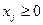 ;
;  (3)
(3)
Змінні 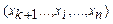 називаються базисними і входять до базисного плану. Через базисні виражаються вільні змінні, які для визначення початкового базисного плану приймаються рівні нулю:
називаються базисними і входять до базисного плану. Через базисні виражаються вільні змінні, які для визначення початкового базисного плану приймаються рівні нулю: 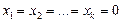 . Тоді базисні змінні будуть рівні
. Тоді базисні змінні будуть рівні 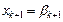 ;
; 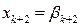 ;…;
;…; 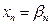 . В такому разі базисний план, тобто розв’язок задачі буде мати вигляд вектора рішень:
. В такому разі базисний план, тобто розв’язок задачі буде мати вигляд вектора рішень: 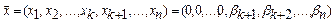 . Він може бути допустимим для
. Він може бути допустимим для 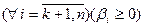 , тобто якщо всі вільні члени системи не від’ємні і
, тобто якщо всі вільні члени системи не від’ємні і 
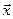 - недопустиме рішення.
- недопустиме рішення.
Для того, щоб знайти оптимальний базисний план, тобто те, коли функція 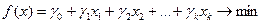 (1) набуде свого мінімального допустимого значення, використовується симплекс-метод – табличний алгоритм заміни базисних змінних.
(1) набуде свого мінімального допустимого значення, використовується симплекс-метод – табличний алгоритм заміни базисних змінних.
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклад 2 | | | Приклад використання симплекс-методу. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |