
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Лабораторне заняття № 15–16
Тема: однофакторний дисперсійний аналіз.
Дисперсійний аналіз якісних ознак.
Мета роботи: ознайомиться зі схемою проведення однофакторного дисперсійного аналізу вибірок з однієї сукупності; навчитися здійснювати оцінку різниці між середніми; освоїти методику проведення дисперсійного аналізу якісних ознак.
Матеріали й устаткування:калькулятор, лінійка, ваги, навчальні посібники, методичний матеріал, гербарні зразки рослин.
Хід роботи
Значно частіше польові і лабораторні досліди мають 10–20 і більше варіантів. У таких випадках попарне їх порівняння стає дуже трудоємким. Якщо дослід складається з k варіантів, то доводиться для оцінки відмінностей між кожною парою середніх провести k(k–1) зіставлень, наприклад для оцінки відмінності між середніми досліду з шістьма варіантами необхідно обчислити 6 помилок і оцінити 15 значень t. Такий шлях оцінки відмінностей між середніми не суперечить теорії статистики, і в деяких випадках до нього доводиться вдаватися. Проте на даний час для оцінки відмінності між варіантами досліду широке застосування знаходить розроблений Р.А. Фішером метод, що отримав назву дисперсійний аналіз.
1. Розкладання дисперсій. Дисперсійний аналіз полягає в розкладанні загальної дисперсії з метою виявити ту її частина, яка обумовлена випадковим варіюванням результатів досліду.
Приклад 1. Вибірки з середньої сукупності. У табл. 34 наведені дані довжини стебла озимої пшениці для чотирьох вибірок по 10 рослин.
Таблиця 34 – Довжина стебла озимої пшениці (у см)
| № вибірок | № рослин | Сума ∑х | Групові середні 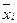
| |||||||||
Загальна сума = 4280.
Розраховуємо суми квадратів за формулою (100):
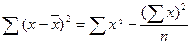 або
або 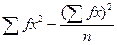 (100).
(100).
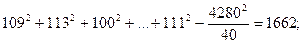
2) суму квадратів для вибірок (всередині вибірок)
№ 1 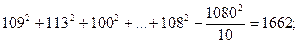
№ 2 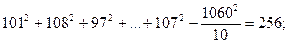
№ 3 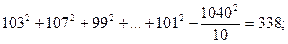
№ 4 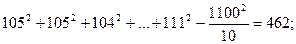
загальна сума 1462.
3) суму квадратів для групових середніх (між вибірками):
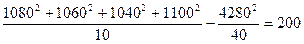
Таким чином, загальна сума квадратів розклалася повністю на складові частини: суму квадратів усередині вибірки і суму квадратів між вибірками. Аналогічним чином число ступенів свободи загальної дисперсії (39) є сумою двох чисел ступенів свободи: 36 – для вибірок і 3 – для групових середніх. Ці дані зведені в таблицю дисперсійного аналізу (табл. 35); цифри останньої графи «Середнім квадратом» є дисперсії відповідних джерел варіювання.
Таблиця 35 – Таблиця дисперсійного аналізу
| Джерело варіювання | Число ступенів свободи | Сума квадратів | Середній квадрат |
| Загальне ………….. | 42,62 | ||
| Між вибірками ....... | 66,67 | ||
| Всередині вибірок.. | 40,61 |
Перевіримо рівність останніх двох дисперсій за допомогою критерію F. Їх відношення дорівнює 66,67:40,61=1,44, зіставимо його з табличним значенням F для 36 і 3 ступенів свободи. Фактичне відношення дисперсій F менше табличного за будь-якого рівня значущості, тому можна вважати дисперсії між вибірками і всередині вибірок однаковими. Таким чином, нульова гіпотеза про приналежність вибірок до однієї сукупності не відкидається, що і слід було чекати, судячи за їх походженням.
Обчислювати суму квадратів окремих видів дисперсії найзручніше за формулами:
загальної 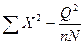 (101)
(101)
між вибірками 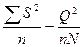 (102)
(102)
де X – окреме спостереження; S – сума спостережень вибірки; Q – загальна сума всіх спостережень; N – число вибірок; n – число спостережень у вибірці.
Якщо вибірки мають різне число спостережень, то суму квадратів загальної дисперсії обчислюють за формулою 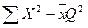 , а між вибірками – за формулою
, а між вибірками – за формулою 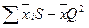 , де
, де 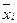 – середні вибірок,
– середні вибірок, 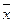 – загальна середня.
– загальна середня.
2. Оцінка відмінності між середніми. Відомо, що внутрішньогрупова дисперсія характеризує випадкове варіювання дослідних даних, статистичним показником якого є середнє квадратичне відхилення.
Знаючи s, можна провести оцінку відмінності між вибірковими середніми. Таку оцінку проводять за допомогою критерію t, визначаючи помилку різниці за формулою (103) при однаковому або за формулою (104) при різному числі спостережень.
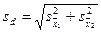 або
або 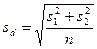 (103)
(103)
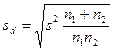 (104)
(104)
Проте при дисперсійному аналізі приймають, що дисперсії, а отже, і помилки групових середніх однакові, тому помилку різниці між будь-якою парою вибірок знаходять не як 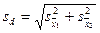 , а за формулами (105) і (106):
, а за формулами (105) і (106):
а) за однакової кількості спостережень:
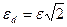 або
або 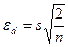 (105)
(105)
де εd – помилка різниці середніх; ε – усереднена помилка загальної середньої досліду 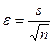 .
.
б) за різної кількості спостережень:
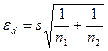 (106)
(106)
де n1 і n2 – число спостережень варіантів, що порівнюються.
Обчислюючи потім для будь-якої пари варіант 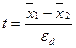 і оцінюючи його звичайним способом порівняння з табличним t, з'ясовують істотність відмінності між вибірковими середніми. Число ступенів свободи беруть з таблиці дисперсійного аналізу для внутрішньогрупової дисперсії.
і оцінюючи його звичайним способом порівняння з табличним t, з'ясовують істотність відмінності між вибірковими середніми. Число ступенів свободи беруть з таблиці дисперсійного аналізу для внутрішньогрупової дисперсії.
Якщо всі варіанти досліду мають однакове число спостережень, замість обчислення декількох значень t знаходять найменшу довірчу (істотну) різницю між середніми:
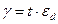 (107)
(107)
і порівнюють з нею попарні різниці. Ті з них, які більше Y, вважають за істотні.
Для прикладу 1 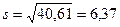 ; звідси
; звідси 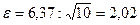 см;
см; 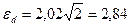 см.
см.
Для 36 ступенів свободи при 5%-ном рівні значущості t=2,03, звідси γ=2,03×2,84=5,77 см. Отже, істотними будуть різниці між вибірками, що перевищують 5,77 см. Як і очікувалося, в даному прикладі немає жодної пари вибірок, що істотно розрізняються за висотою стебла. Відмінності між ними знаходяться, як прийнято говорити, в межах помилки досліду.
3. Дисперсійний аналіз якісних ознак. Викладені в попередніх параграфах принципи дисперсійного аналізу можуть застосовуватися і при порівнянні декількох вибірок якісних ознак. Дисперсія якісної ознаки 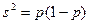 , де р – частка одиниць вибірки, яким властива ця ознака. Коли р виражене у відсотках, то
, де р – частка одиниць вибірки, яким властива ця ознака. Коли р виражене у відсотках, то 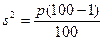 .
.
Суми квадратів і числа з ступенів свободи загальної дисперсії і дисперсії між вибірками розраховують за формулами, наведеними в табл. 36, а внутрішньогрупової (випадковою) дисперсії – за різницею.
Таблицям 36 – Схема дисперсійного аналізу якісних ознак
| Дисперсії | р у частках одиниці | р в % | ||
| сума квадратів | число ступенів свободи | сума квадратів | число ступенів свободи | |
| Загальна | 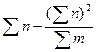
| 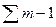
| 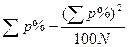
| 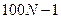
|
| Вибірок | 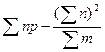
| 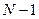
| 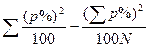
| 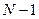
|
Примітка. У цих формулах m позначає загальне число екземплярів в окремих вибірках, n – число екземплярів, якім властива дана ознака, 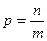 – частку ознаки, р% – частку ознаки у відсотках, N – загальне число вибірок.
– частку ознаки, р% – частку ознаки у відсотках, N – загальне число вибірок.
Приклад 1. Щоб викласти техніку дисперсійного аналізу якісних ознак, користуються даними про уражуваності ярової пшениці твердою сажкою при штучному зараженні залежно від умов живлення. Дослід проводили з трьома сортами, які протягом трьох років вирощували на наступних фонах:
0 – без добрива;
1 – удобрення гноєм 60 т на 1 га.
2 – удобрення N30Р45К45;
3 – NPK + 15 кг на 1 га хлористого натрію;
4 – NPK + 2 кг на 1 га бору;
5 – NPK + 5 кг на 1 га сірчанокислої міді;
6 – NPK на 4 кг на 1 га сірчанокислого цинку;
7 – NPK + 30 кг на 1 га марганцевокислого калію
У табл. 37 наведені дані досліду в середньому за трьома сортами:
Таблиця 37 – Уражуваність ярової пшениці твердою сажкою (у %)
| Фон живлення | |||||||
| 1-й | 2-й | 3-й | 4-й | 5-й | 6-й | 7-й | |
Обчислення сум квадратів зручніше проводити так, як показано в табл. 38 і 39.
Обчислюємо суми квадратів:
загальній дисперсії 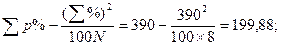
дисперсії між вибірками 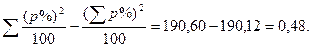
Таблиця 38 – Обчислення сум квадратів
| Вибірка | ∑ | ||||||||
| р% | |||||||||
| (р%)2 | - | ||||||||
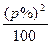
| 28,09 | 24,01 | 23,04 | 21,16 | 20,25 | 25,00 | 26,01 | 23,04 | 190,60 |
Таблиця 39 – Таблиця дисперсійного аналізу
| Дисперсія | Число ступенів свободи | Сума квадратів | Середній квадрат | Fфакт | Fтабл | |
| 0,05 | 0,01 | |||||
| Загальна | 199,88 | |||||
| Варіантів | 0,48 | 0,0686 | 0,27 | 3,23 | 5,65 | |
| Залишкова (випадкова) | 199,40 | 0,2518 |
Так як Fфакт<Fтабл, відмінності між різними способами дії, що спостерігалися в досліді не можна визнати істотними; внаслідок цього необхідність в оцінці конкретних відмінностей між окремими варіантами досвіду відпадає.
Приклад 2. У табл. 40 приведені дані про польову схожість шести зразків кукурудзи і розрахунки для обчислення сум квадратів.
Сума квадратів:
загальній дисперсії 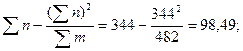
дисперсії варіантів 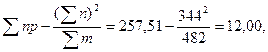
Перевірка дисперсій за допомогою критерію F свідчить про наявність істотних відмінностей між зразками.
Переходячи до оцінки відмінності між порівнюваними долями, нагадаємо, що для цього використовують критерій 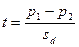 . При звичайній попарній оцінці відмінностей між долями sd знаходять за формулою (108).
. При звичайній попарній оцінці відмінностей між долями sd знаходять за формулою (108).
Таблиця 40 – Польова схожість насіння кукурудзи і розрахунки для обчислення сум квадратів
| Показники | № зразка | ||||||
| сума | |||||||
| Посіяно насіння (m) | |||||||
| Зійшло насіння (n) | |||||||
| p=n:m ……………. | 0,80 | 0,67 | 0,54 | 0,85 | 0,94 | 0,50 | |
| Np ……………….. | 51,20 | 38,19 | 22,68 | 62,90 | 62,04 | 20,50 | 257,51 |
Дисперсійний аналіз наведений у табл. 41.
Таблиця 41 – Дисперсійний аналіз
| Дисперсія | Число ступенів свободи | Сума квадратів | Середній квадрат | Fфакт | Fтабл | |
| 0,05 | 0,01 | |||||
| Загальна | 98,49 | |||||
| Варіантів | 12,00 | 2,400 | 13,18 | 2,23 | 3,06 | |
| Залишкова (випадкова) | 86,49 | 0,182 |
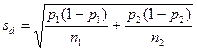 (108)
(108)
При дисперсійному аналізі якісних ознак εd визначають так само, як і для кількісних ознак. Проведемо відповідні обчислення.
1. Середня квадратична помилка частки 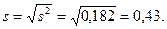
2. Помилка середньої частки 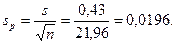
3. Середня помилка різниці доль 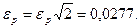
4. Довірча різниця: для 5%-ного рівня 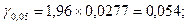 для 1%-ного рівня
для 1%-ного рівня 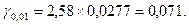
При 5%-ном рівні значущості неістотно розрізняються за польовою схожістю тільки пари зразків: 1 – 4 і 3 – 6.
| <== попередня сторінка | | | наступна сторінка ==> |
| II. Практичне завдання. | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |