
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Теорема. Кожна скінчена гра має принаймні один оптимальний розв’язок, можливо, серед мішаних стратегій.
Ця теорема має велике практичне значення – вона дає конкретні моделі знаходження оптимальних стратегій при відсутності сідлової точки.
Розглянемо гру розміру 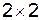 , яка є найпростішим прикладом скінченої гри. Якщо така гра має сідлову точку, то оптимальний розв’язок – це пара чистих стратегій, що відповідають цій точці.
, яка є найпростішим прикладом скінченої гри. Якщо така гра має сідлову точку, то оптимальний розв’язок – це пара чистих стратегій, що відповідають цій точці.
Гра, в якій відсутня сідлова точка, у відповідності з основною теоремою, має оптимальний розв’язок, що визначається парою мішаних стратегій 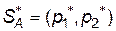 і
і 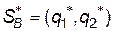 .
.
Для того щоб знайти їх, скористаємось теоремою про активні стратегії. Якщо гравець  притримується своєї оптимальної стратегії
притримується своєї оптимальної стратегії 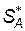 , то його середній виграш буде рівним ціні гри
, то його середній виграш буде рівним ціні гри 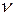 , якою б активною стратегією не користувався гравець
, якою б активною стратегією не користувався гравець  . Для гри
. Для гри 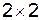 будь-яка чиста стратегія противника є активною, якщо відсутня сідлова точка. Виграш гравця
будь-яка чиста стратегія противника є активною, якщо відсутня сідлова точка. Виграш гравця  (програш гравця
(програш гравця  ) – випадкова величина, математичне сподівання (середнє значення) якої є ціною гри. Тому середній виграш гравця
) – випадкова величина, математичне сподівання (середнє значення) якої є ціною гри. Тому середній виграш гравця  ( оптимальна стратегія ) буде дорівнювати
( оптимальна стратегія ) буде дорівнювати 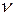 і для першої і для другої стратегії супротивника.
і для першої і для другої стратегії супротивника.
Нехай гра задана платіжною матрицею 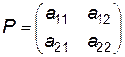 .
.
Середній виграш гравця  , якщо він використає оптимальну мішану стратегію
, якщо він використає оптимальну мішану стратегію 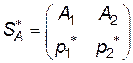 , а гравець
, а гравець  -- стратегію
-- стратегію 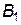 дорівнює ціні гри
дорівнює ціні гри 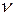 :
:
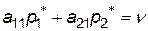 .
.
Такий же виграш і при застосуванні другим гравцем стратегії 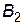 , тобто
, тобто
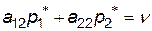 .
.
Враховуючи, що 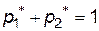 , одержимо систему рівнянь для визначення оптимальної стратегії
, одержимо систему рівнянь для визначення оптимальної стратегії 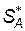 і ціни гри
і ціни гри 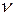 :
:
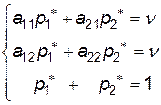 ( 12.1 )
( 12.1 )
Розв’язуючи цю систему, одержимо оптимальну стратегію
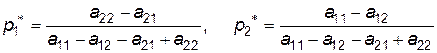
і ціну гри
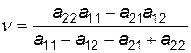 .
.
Застосовуючи теорему про активні стратегії для знаходження 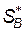 -- оптимальної стратегії гравця
-- оптимальної стратегії гравця  , одержимо, що при будь-якій чистій стратегії гравця
, одержимо, що при будь-якій чистій стратегії гравця  (
( 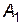 чи
чи 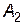 ) середній програш гравця
) середній програш гравця  дорівнює ціні гри
дорівнює ціні гри 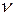 , тобто
, тобто
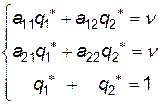 ( 12.2 )
( 12.2 )
Тоді оптимальна стратегія 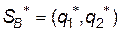 визначається формулами
визначається формулами
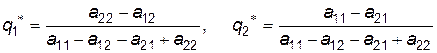
Приклад. Застосуємо одержані результати для знаходження оптимальних стратегій для гри «Пошук»:
Розв’язок. Гра «Пошук» задана платіжною матрицею без сідлової точки:
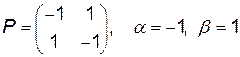 .
.
Шукаємо розв’язок в мішаних стратегіях. Для гравця  середній виграш дорівнює ціні гри
середній виграш дорівнює ціні гри 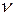 (при
(при 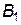 і
і 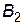 ); для гравця
); для гравця  середній програш дорівнює ціні гри
середній програш дорівнює ціні гри 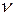 (при
(при 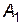 і
і 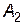 ). Системи рівнянь мають вигляд:
). Системи рівнянь мають вигляд:
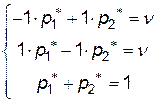
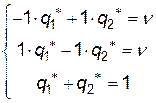 ( 12.3 )
( 12.3 )
Розв’язуючи ці системи, одержуємо 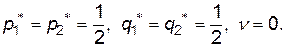 Це означає, що оптимальна стратегія кожного гравця полягає в тому, щоб чергувати свої чисті стратегії випадковим чином, вибираючи кожне із сховищ з імовірністю
Це означає, що оптимальна стратегія кожного гравця полягає в тому, щоб чергувати свої чисті стратегії випадковим чином, вибираючи кожне із сховищ з імовірністю 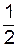 . При цьому середній виграш дорівнює 0.
. При цьому середній виграш дорівнює 0.
5. Зведення гри 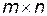 до двоїстої пари ЗЛП.
до двоїстої пари ЗЛП.
Гра 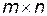 може бути зведена до розв’язання задачі лінійного програмування.
може бути зведена до розв’язання задачі лінійного програмування.
Нехай гра 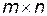 задана платіжною матрицею
задана платіжною матрицею 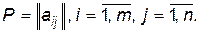 Гравець
Гравець  володіє стратегіями
володіє стратегіями 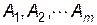 , гравець
, гравець  -- стратегіями
-- стратегіями 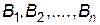 . Необхідно визначити оптимальні стратегії
. Необхідно визначити оптимальні стратегії 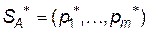 і
і 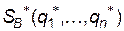 , де
, де 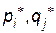 -- імовірності застосування відповідних чистих стратегій
-- імовірності застосування відповідних чистих стратегій 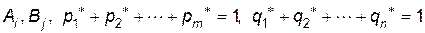 .
.
Оптимальна стратегія 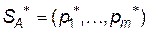 задовольняє вимогу: забезпечує гравцю
задовольняє вимогу: забезпечує гравцю  середній виграш, не менший ніж ціна гри
середній виграш, не менший ніж ціна гри 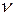 , при будь-якій стратегії гравця
, при будь-якій стратегії гравця  і виграш, рівний ціні гри
і виграш, рівний ціні гри 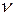 , при оптимальній стратегії гравця
, при оптимальній стратегії гравця  . Нехай
. Нехай 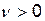 ( цього можна досягти зробивши всі елементи
( цього можна досягти зробивши всі елементи 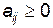 ). Якщо гравець
). Якщо гравець  застосовує мішану стратегію
застосовує мішану стратегію 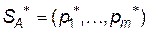 проти будь-якої чистої стратегії
проти будь-якої чистої стратегії 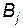 гравця
гравця  то одержить середній виграш ( математичне сподівання виграшу )
то одержить середній виграш ( математичне сподівання виграшу )
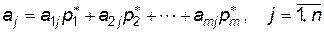
Для оптимальної стратегії 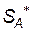 всі середні виграші не менші ціни гри
всі середні виграші не менші ціни гри 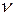 , тому отримаємо систему нерівностей:
, тому отримаємо систему нерівностей:
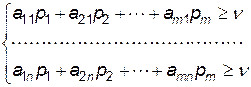 ( 12.4 )
( 12.4 )
Кожну з нерівностей поділимо на 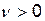 і введемо нові змінні:
і введемо нові змінні: 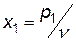 ,
,  ,
, 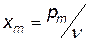 . Тоді система ( 12.4 ) матиме вигляд
. Тоді система ( 12.4 ) матиме вигляд
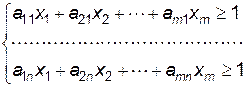 ( 12.5 )
( 12.5 )
Ціль гравця  -- максимізувати свій гарантований виграш, тобто ціну гри
-- максимізувати свій гарантований виграш, тобто ціну гри 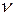 . Поділивши на
. Поділивши на 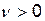 рівність
рівність 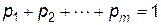 , одержуємо, що змінні
, одержуємо, що змінні 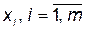 задовольняють умові:
задовольняють умові: 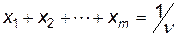 . Максимізація ціни гри
. Максимізація ціни гри 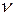 еквівалентна мінімізації величини
еквівалентна мінімізації величини 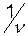 , тому задачу можна сформулювати наступним чином:
, тому задачу можна сформулювати наступним чином:
Визначити значення змінних 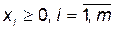 так, щоб вони задовольняли лінійним обмеженням ( 12.5 ) і при цьому лінійна функція Z досягала свого мінімального значення
так, щоб вони задовольняли лінійним обмеженням ( 12.5 ) і при цьому лінійна функція Z досягала свого мінімального значення
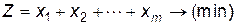 ( 12.6 )
( 12.6 )
Це задача лінійного програмування.
Розв’язуючи задачу ( 12.5 ) – ( 12.6 ) одержимо оптимальний розв’язок 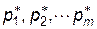 і оптимальну стратегію
і оптимальну стратегію 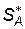 .
.
Для визначення оптимальної стратегії 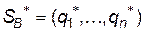 слід врахувати, що гравець
слід врахувати, що гравець  намагається мінімізувати гарантований виграш, тобто знайти
намагається мінімізувати гарантований виграш, тобто знайти 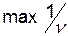 . Змінні
. Змінні 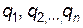 задовольняють системі нерівностей:
задовольняють системі нерівностей:
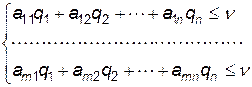 ( 12.7 )
( 12.7 )
які випливають з того, що середній програш гравця  не перевищує ціни гри, яку б чисту стратегію не застосував гравець
не перевищує ціни гри, яку б чисту стратегію не застосував гравець  .
.
Якщо позначити 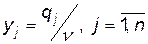 , то одержимо систему нерівностей:
, то одержимо систему нерівностей:
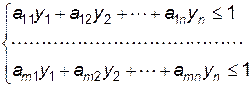 ( 12.8 )
( 12.8 )
Змінні 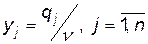 задовольняють умові:
задовольняють умові:  .
.
Гра звелась до наступної задачі:
Визначити значення змінних 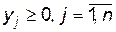 , які задовольняють системі нерівностей ( 12.8 ) і максимізують лінійну функцію
, які задовольняють системі нерівностей ( 12.8 ) і максимізують лінійну функцію
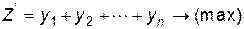 ( 12.9 )
( 12.9 )
Розв’язок задачі лінійного програмування (12.8)-(12.9) визначає оптимальну стратегію 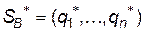 . При цьому ціна гри
. При цьому ціна гри
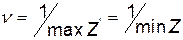 . ( 12.10 )
. ( 12.10 )
Порівнюючи задачі (12.5) – (12.6) і (12.8) – (12.9), впевнюємось, що вони є взаємно-двоїстими. При розв’язуванні конкретних задач слід вибрати ту, розв’язок якої більш простіший, а розв’язок іншої знайти за теоремою двоїстості.
Наведемо приклади економічних задач, які описуються ігровими моделями 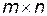 і можуть бути розв’язані методами лінійного програмування.
і можуть бути розв’язані методами лінійного програмування.
Приклад. Підприємство може випускати три види продукції 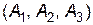 , одержуючи при цьому прибуток, який може бути в одному з трьох станів
, одержуючи при цьому прибуток, який може бути в одному з трьох станів 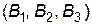 . Задана платіжна матриця, її елементи характеризують прибуток, який одержить підприємство при випуску продукції
. Задана платіжна матриця, її елементи характеризують прибуток, який одержить підприємство при випуску продукції 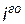 виду з
виду з 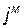 станом попиту:
станом попиту:
| Попит Прод. | 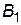
| 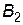
| 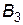
| 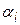
|
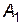
| ||||
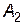
| ||||
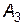
| ||||
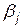
|
Визначити оптимальні пропорції в виробництві продукції, що гарантують середню величину прибутку при будь-якому стані попиту, вважаючи його невизначеним.
Розв’язок. Задача зводиться до ігрової моделі, в якій гра підприємства  проти попиту
проти попиту  задана платіжною матрицею
задана платіжною матрицею 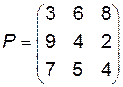 .
.
Визначимо нижню та верхню ціну гри: 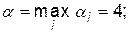
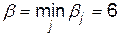 . Так як
. Так як 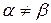 , то сідлова точка відсутня і оптимальний розв’язок слід шукати в мішаних стратегіях гравців:
, то сідлова точка відсутня і оптимальний розв’язок слід шукати в мішаних стратегіях гравців: 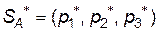 і
і 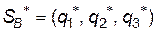 . Позначивши
. Позначивши 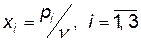 ,
, 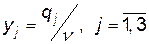 , складемо дві взаємно-двоїсті задачі лінійного програмування:
, складемо дві взаємно-двоїсті задачі лінійного програмування:
| Задача 1 | Задача 2 |
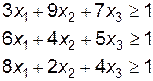
| 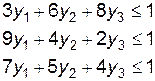
|
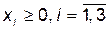
| 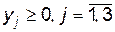
|
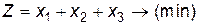
| 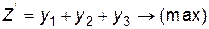
|
Розв’язуємо симплексним методом одну із задач, наприклад, задачу 2, оскільки для неї легко знайти початковий опорний план. Запишемо основну систему обмежень (ОСО) в канонічному вигляді:
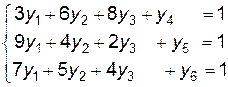
I крок. Ортонормований базис складають вектори 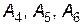 . Базисні змінні -
. Базисні змінні - 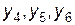 ; вільні змінні -
; вільні змінні - 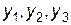 . Початковий опорний план має вигляд
. Початковий опорний план має вигляд
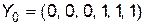 .
.
Складемо першу симплексну таблицю і перевіримо умови оптимальності:
| Б | 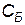
| 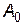
| 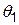
| 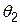
| 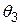
| ||||||
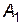
| 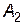
| 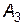
| 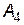
| 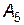
| 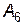
| ||||||
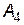
| 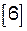
| 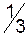
| 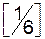
| 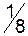
| |||||||
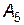
| 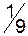
| 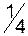
| 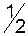
| ||||||||
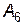
| 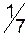
| 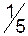
| 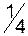
| ||||||||
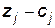
| -1 | -1 | -1 |
План 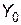 не є оптимальним, так як серед оцінок векторів є від’ємні. Перейдемо до нового опорного плану. Введемо до базису вектор
не є оптимальним, так як серед оцінок векторів є від’ємні. Перейдемо до нового опорного плану. Введемо до базису вектор 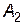 на місце вектора
на місце вектора 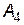 .
.
Складемо другу симплексну таблицю:
| Б | 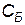
| 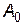
| 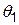
| ||||||
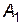
| 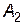
| 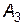
| 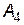
| 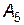
| 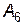
| ||||
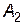
| 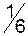
| 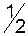
| 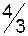
| 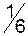
| 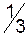
| ||||
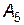
| 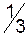
| 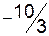
| 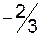
| 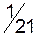
| |||||
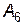
| 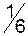
| 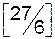
| 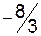
| 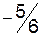
| 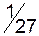
| ||||
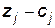
| 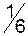
| 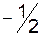
| 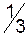
| 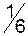
|
Опорний план 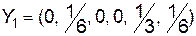 не є оптимальним, так як оцінка вектора
не є оптимальним, так як оцінка вектора 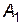 від’ємна. Вектор
від’ємна. Вектор 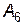 виведемо з базису, а на його місце введемо вектор
виведемо з базису, а на його місце введемо вектор 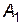 . Складемо наступну симплексну таблицю:
. Складемо наступну симплексну таблицю:
| Б | 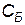
| 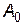
| ||||||
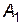
| 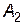
| 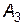
| 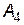
| 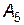
| 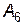
| |||
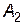
| 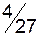
| 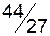
| 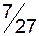
| 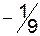
| ||||
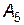
| 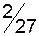
| 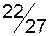
| 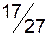
| 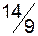
| ||||
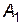
| 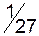
| 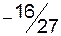
| 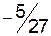
| 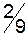
| ||||
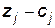
| 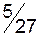
| 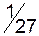
| 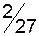
| 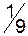
|
Всі оцінки невід’ємні, отже, план 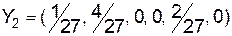 - оптимальний план,
- оптимальний план, 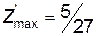 .
.
Встановимо відповідність між змінними взаємно-двоїстих задач і визначимо оптимальний розв’язок задачі 1 за допомогою теорем двоїстості та даних індексного рядка останньої симплексної таблиці:
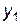
| 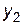
| 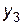
| 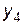
| 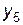
| 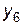
| |||
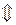
| 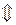
| 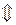
| 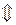
| 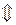
| 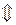
| |||
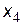
| 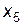
| 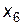
| 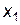
| 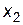
| 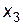
| |||
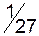
| 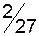
| 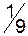
|
Оптимальний розв’язок задачі 1: 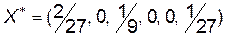 , причому
, причому 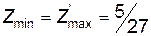 . Із співвідношень (12.10) знаходимо ціну гри
. Із співвідношень (12.10) знаходимо ціну гри 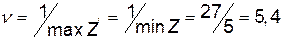 .
.
Зауважимо, що оптимальний розв’язок двоїстої задачі можна знайти за формулою: 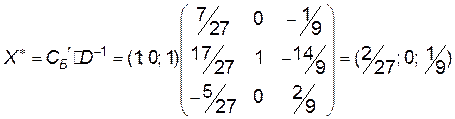 .
.
Оптимальну стратегію випуску продукції 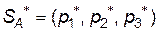 знайдемо, скориставшись співвідношенням
знайдемо, скориставшись співвідношенням 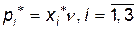 , тобто
, тобто
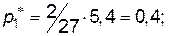
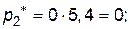
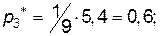
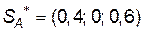 .
.
Отже підприємство повинно випустити 40% продукції 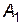 і 60% продукції
і 60% продукції 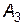 , а продукцію
, а продукцію 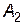 взагалі не випускати.
взагалі не випускати.
Оптимальна стратегія попиту 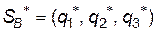 визначається аналогічно:
визначається аналогічно: 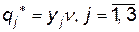 , тобто
, тобто 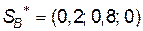 . Таким чином, оптимальний попит в 20% знаходиться в стані
. Таким чином, оптимальний попит в 20% знаходиться в стані 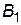 і 80% - в стані
і 80% - в стані 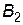 .
.
При розв’язуванні довільної скінченої гри розміром 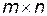 рекомендується притримуватись наступнох схеми:
рекомендується притримуватись наступнох схеми:
1. Виключити з платіжної матриці завідомо невигідні стратегії в порівнянні з іншими стратегіями. Такими стратегіями для гравця  (гравця
(гравця  ) є ті, яким відповідають рядки (стовпці) з елементами меншими (більшими) в порівнянні з елементами інших рядків (стовпців).
) є ті, яким відповідають рядки (стовпці) з елементами меншими (більшими) в порівнянні з елементами інших рядків (стовпців).
2. Визначити верхню і нижню ціну гри і перевірити чи має гра сідлову точку. Якщо сідлова точка є, то відповідні їй стратегії гравців будуть оптимальними, а ціна співпадає з верхньою (нижньою) ціною.
3. Якщо сідлова точка відсутня, то розв’язок слід шукати в мішаних стратегіях. Для гри розміру 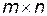 рекомендується симплексний метод, а для гри розміру
рекомендується симплексний метод, а для гри розміру 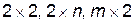 - графо-аналітичний метод.
- графо-аналітичний метод.
| <== попередня сторінка | | | наступна сторінка ==> |
| Розв’язування гри в мішаних стратегіях. | | | Світове господарство: сутність та структура |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |