• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Рішення

Представимо функціональну модель задачі у наступному вигляді (рис.7.2)

Y₁ θ₁ Y₂ θ₂ Y₅ θ₅

K₁ K₂ K₅ φ₅

X₁ X₂ X₅

Вузловими точками моделі є точки розподілу суми коштів K_t між підприємствами. Практично це початок кожного календарного року. Таких кроків буде 5. Далі для спрощення виразимо у; через 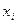тобто 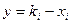. Записуємо функцію переходу 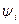виграш 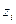, для кожного з етапів, починаючи, як це витікає з методу ДП, з п'ятого (останнього) етапу.

Етап 5

З огляду на те, що y_s=k_i-x_i і враховуючи а=0,4 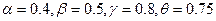запишемо рівняння переходу:

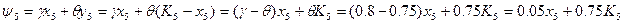
За умовою цей залишок у прибуток не включається.

Величина отриманого прибутку протягом цього року:

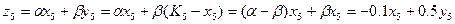
Шукаємо максимум цього прибутку

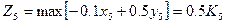- якщо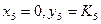

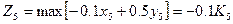- якщо .

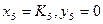Етап 4

Робимо аналогічні дії:

,

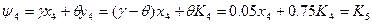оскільки це те, що залишилося після 4го року.

,

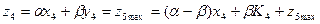тому що прибуток за четвертий рік додається до прибутку 5-го року. Враховуючи, що 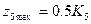: Z₄=max (-0,1х₄+0,5К₄+0,5К₅).

Підставимо значення К₅ і отримаємо для сумарного прибутку за 4-й і 5-й роки:

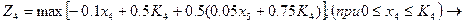
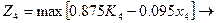
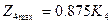
Етап 3

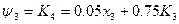
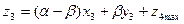
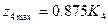
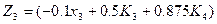
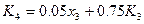
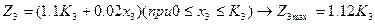
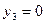
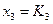
Етап 2

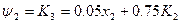
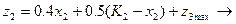
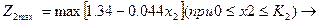
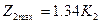
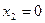
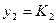
Етап1

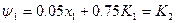
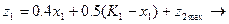
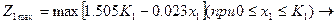
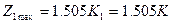
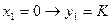
Отже: максимальний прибуток діяльності 2-х підприємств за 5 років буде дорівнювати 1,505 від суми первісного вкладення, якщо на 1 і 2 роках усю суму капіталовкладень вкладати в друге підприємство, на 3-му році в перше, а на 4 і 5 роках - знову в друге підприємство. Така стратегія оптимального управління розвитком 2х підприємств.

Досі ми розглядали простий випадок, коли а і β однакові для всіх етапів. Зустрічаються задачі, де а і β на кожному етапі різні (це є задача розподілу ресурсів з неоднорідними етапами). Рішення цієї задачі практично не відрізняється від розглянутої раніше і вирішується аналогічно із застосуванням поточних значень а_і і β_і, на кожному і-му році розвитку підприємства.

Зустрічаються також задачі розподілу ресурсів, коли отриманий прибуток відчисляється не повністю, а частково вкладається в розвиток виробництва. У цьому випадку відрахований прибуток на будь-якому і-му кроці записується у виді:

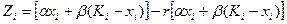
де г - коефіцієнт, який характеризує частину прибутку, що вкладається в

розвиток виробництва.

Основне функціональне рівняння при цьому приймає вид: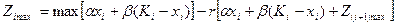

В подальшому процедура рішення залишається незмінною.

Якщо розглядається задача розподілу ресурсів між п об'єктами господарської діяльності, то приходиться на кожнім кроці мати п оптимальних рішень (але не 2 , як ми розглядали).

Тоді и_і=(x_і⁽¹⁾ x_і⁽²⁾. . . x_і^(п) ) - вектор вкладень в підприємства на початок г-го року.

Процес пошуку оптимальної стратегії управління вкладеннями на кожному кроці також зважується поетапно. Стан системи перед початком кожного етапу як і раніше буде характеризуватися одним числом (К_і) (і = (1,т), т-число етапів). Складніше буде с вибором управлінь (капіталовкладень в к-е підприємство на кожному і-му етапі х_і^к).

Необхідно виконати наступні умови на і-му кроці: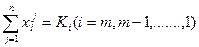

При цьому основне функціональне рівняння матиме вид

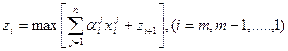
Це вже класична задача ЛП, розв'язання якої вже розглядалося у попередньому розділі, що має вирішуватися для кожного j'-го кроку.

Досить часто в практиці приходиться вирішувати задачу розподілу ресурсів із вкладенням прибутку в розвиток виробництва. Подібні задачі називаються виродженими. Особливістю їх є те, що вони вирішуються з першого до останнього кроку, (тільки вперед), що значно спрощує процедуру рішення.

Наприклад, для закупівлі устаткування 2-х типів, виділена сума 20000грн.. Ефективність вкладення цих засобів в устаткування оцінюється тим прибутком, що одержить підприємство, використовуючи це устаткування.

Нехай для устаткування 1-го типу коефіцієнт ефективності (прибутку) складає α₁= 0,4; для 2-го типу α₂=0,42. Наприкінці звітного періоду використане устаткування реалізується за ціною 0,7 і 0,6 первісної вартості (коефіцієнти амортизації відповідно β₁=0,7 і β₂=0,6). Отримані від продажу кошти, а також отриманий прибуток знову вкладаються в придбання устаткування 1-го і 2-го типів.

Ставиться задача знайти оптимальний розподіл коштів для їх закупівлі протягом 3-х років.

Переглядів: 326