
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Типові графи станів СМО
При описі процесів функціонування СМО найбільш поширеними є типові структури "блукання" (процес "загибелі та розмноження"), а також циклічна структура. Розглянемо кожну з цих структур. Процес "загибелі та розмноження"
|
|
|
|

Рисунок 8. 3. Граф станів процесу «загибелі та розмноження»
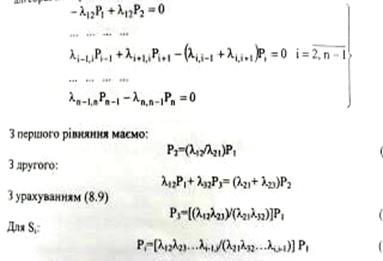 Перехід в стан Sі+1 відповідає народженню, перехід в стан Sі-1 — загибелі одної особи популяції. Якщо λіj=const і п — певне натуральне число, то для сталого режиму цього процесу можна записати систему алгебраїчних рівнянь у вигляді:
Перехід в стан Sі+1 відповідає народженню, перехід в стан Sі-1 — загибелі одної особи популяції. Якщо λіj=const і п — певне натуральне число, то для сталого режиму цього процесу можна записати систему алгебраїчних рівнянь у вигляді:
Усі імовірності Р, виражено через початкову Рі, значення якої можна отримати з урахуванням нормованого рівняння
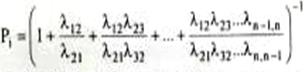
Таким чином, для марковського процесу "загибелі та розмноження", знаючи лише інтенсивності усіх переходів, можна визначити імовірності знаходження СМО в кожному з станів.
Розглянемо в якості прикладу одноканальну мобільну АЗС, що встановлюється вздовж дороги. Додатково умовимось, що якщо АЗС зайнята, інші автомобілі, які мають заправитись, від'їжджають в пошуках іншої вільної АЗС. Середня інтенсивність прибуття автомобілів для заправки λ=0,8 од/хв.
Середній час заправки tcp = 1,5хв. Необхідно визначити імовірності станів СМО в перехідному та сталому режимах
Рішення.
СМО має два можливих стани: So – АЗС вільна, S1 – АЗС зайнята. Якщо автомобіль надходить, коли СМО у стані S1, то він не обслуговується. Граф станів має вигляд рис. 8. 4. І представляє собою найпростіший ланцюг "загибелі та розмноження" з 2-ма станами.
| λ | |||
| So | S1 | ||
| µ |
Перехід з So до S1 здійснюється з інтенсивністю λ, зворотній перехід з інтенсивністю обслуговування (µ=l/tcp =0,366 обс/хв.
Запишемо рівняння Колмогорова. Оскільки нормовочне рівняння є
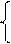 Р1(t)+P2(t)=1, то при п=2 слід записати тільки одне рівняння:
Р1(t)+P2(t)=1, то при п=2 слід записати тільки одне рівняння:
dP1(t)/dt=λP0(t)-µP1(t)
Р1(t)+P2(t)=1
З цього рівняння маємо:

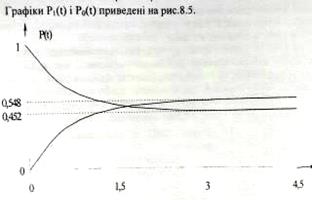
Рис.8.5 Графіки змін ймовiрностей станів в одноканальній СМО з відмовами
Нескладно побачити, що для будь-якого моменту часу t має місце рівність
P1(t) + P0(t)=l
Для сталого (граничного) режиму (t—>оо)
P0=µ/λ+µ=0.452 P1=λ/λ+µ=0.548
Тобто в сталому режимі АЗС приблизно 45,2% часу роботи буде вільною, а 54,8% робочого часу буде зайнята.
Циклічний процес.
Неперервний марковський ланцюг називається циклічним процесом, якщо стани зв'язані між собою в кільце (цикл) з однобічними зв'язками (див. рис.8.6)

Рис.8.6. Граф станів циклічного процесу.
Для цього марковського ланцюга, що має визначену кількість станів та можливість усіх переходів, сталий (граничний) режим також існує. Визначимо його за допомогою рівнянь Колмогорова.
λn,1Р1 = λ12Р1
… … … …
λi-1,iРi-1 = λi,i+1Рi (8.14)
… … … …
λn-1,nРn-1 = λn,1Рn
Визначаємо усі Pi (і =2,п) через Р1

Тоді формули (8.15) з урахуванням (8.16) можна представити у вигляді:

Розглянемо приклад циклічного марковського процесу.
Вантажний автомобіль працює безвідмовно у середньому 30 діб, середній час знаходження автомобіля у ремонті складає 1 добу. Після ремонту він має бути підготовлений до роботи протягом 0,2 доби. Знайти граничні імовірності усіх станів автомобіля.
Рішення.
Процес перебування автомобіля в роботі, ремонті та післяремонтній підготовці є циклічним процесом, що має 3 стани.
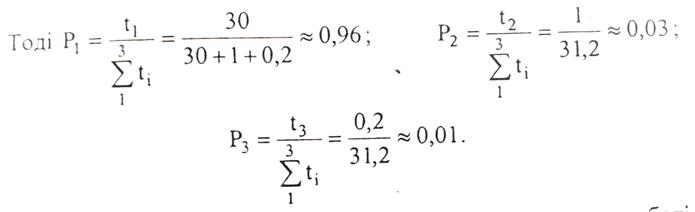
Таким чином, зі 100% загального часу знаходження в роботі він є працездатним протягом 96% загального терміну роботи, 3% — в ремонті і 1% — впідготовчому до роботи періоді.
| <== попередня сторінка | | | наступна сторінка ==> |
| Формалізація СМО марковськими випадковими процесами | | | Пуассонівські СМО розімкнутого типу |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |