
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Пуассонівські СМО розімкнутого типу
Вцьому розділі розглядаються лише методи аналізу СМО, що мають стаціонарні пуассонівські вхідний і вихідний потоки вимог і обслуговувань. Такі СМО в літературі називаються іноді пуассонівськими (найпростішими) СМО (по типу потоків, що розглядаються). Оскільки нхідний і вихідний потоки є пуассонівськими, тобто без післядії, для аналізу найпростіших СМО найбільш придатними є методи аналізу марковських ланцюгів, розглянутих у попередньому розділі. Найпростіші СМО у своїй більшості відповідають процесу "загибелі і розмноження", який є найбільш поширеною моделлю подібних СМО.
Нагадаємо, що СМО є розімкнутою (відкритою), якщо в ній кількість джерел, що формують вхідний потік вимог на обслуговування не і обмеженою і не залежить від стану СМО. Навпаки, в замкнених СМО кількість джерел обмежена і зміни в стані СМО суттєво впливають на інтенсивність вхідного потоку. В цьому розділі розглядатимуться тільки розімкнуті СМО.
8.6.1. Загальний підхіддо аналізу СМО
Нехай СМО розімкнутого типу містить п однотипних каналів обслуговування, кожен з яких характеризується експоненціальним розподілом значень часу обслуговування з середнім значенням to6c, що еквівалентно інтенсивності потоку обслуговувань µ=1 /to6c, /незалежно від типу замовлення, що обслуговується.
При повністю завантажених каналах вимоги на обслуговування можуть чекати у загальній черзі з числом місць чекання m. Дисципліна обслуговування є безпріоритетною (FIFO - First Input First Output). Заявки на вході СМО відносяться до одного з М типів, причому заявки j-того типу ( і = 1,М) створюють найпростіший потік з інтенсивністю λі. Очевидно, що в цьому випадку при умові безпріоритетності обслуговування заявок загальний вхідний потік дорівнює λ=Sλі
Будемо вважати деякі заявки "нетерплячими", тобто такими, що перебувають в СМО не більше tдоп одиниць часу. Якщо час перебування перевищує tД0П, то заявка залишає СМО необслуженою і вважається втраченою, створюючи цим самим потік втрат СМО. Будемо вважати, що tдоп є також випадковою величиною з експоненціальною щільністю розподілу часу перебування f(tдоп) і значенням математичного очікування середнього¯tдon . Таким чином, можна говорити, що потік втрат СМО є найпростішим із інтенсивністю ν=1/ ¯tдon. При цьому можливі втрати як з черги чекання (коли tчек ³ tдon), так і з каналу обслуговування (коли tобс ³ tдon). Методично зручніше розрізняти два потоки втрат:
- до моменту початку обслуговування з інтенсивністю νчек
- після початку обслуговування з інтенсивністю νобс
Враховуючи, що момент призначення заявки на обслуговування випадково призначається на інтервалі між сусідніми моментами покидання черги заявками, то відрізок часу як між моментами надходження заявок у чергу і її можливого покидання черги, так і між початком обслуговування і моментом можливого відходу заявки в процесі обслуговування, будуть мати однаковий експоненціальний розподіл з математичним очікуванням ¯tдоn . Причиною цього явища є властивість відсутності післядії, якою володіють саме найпростіші потоки. Тому вважатимемо, що
νчек= νобс =ν=1/ ¯tдon.
Така СМО є досить загальною структурою, з якою можна, прирівнюючи деякі параметри або до нуля, або до одиниці, або до нескінченості, отримати часткові типи СМО, тому отримаємо спочатку загальні формули аналізу СМО, з наступним їх спрощенням для окремих часткових випадків.
Граф станів розглянутої СМО із застосуванням марковського процесу "загибелі та розмноження" представлений на рис.8.7.
В цьому графі: So — в СМО немає заявок на обслуговування (СМО вільна); Si — в СМО є тільки одна заявка, що обслуговується, черги немає; Sn — усі п каналів обслуговування СМО зайняті, але черги немає; Sn+, — п каналів обслуговування СМО зайняті, одна заявка в черзі чекання; Sn+m — п каналів обслуговування зайняті, m заявок в черзі чекання. В цьому випадку чергова заявка, що надходить в СМО, отримає відмову в обслуговуванні і залишить СМО.
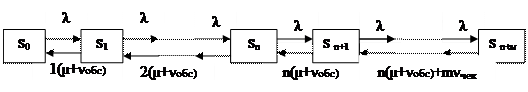
Рис.8.7. Узагальнений граф станів найпростішої СМО розімкненого типу.
Інтенсивність потоку завантаження ("розмноження"), що переводить СМО зі стану Sі до стану Sі+1 (верхні стрілки переходів на рис.8.7) дорівнює інтенсивності вхідного потоку λ, тому що збільшення заявок в системі можливе саме за рахунок вхідного потоку.
Інтенсивність же потоку розвантаження (нижні стрілки переходів на рис.8.7) міняються в залежності від стану СМО. Якщо обслуговуванням заявок зайнятий будь-який один канал (стан S1), то інтенсивність потоку розвантаження обслужених заявок µ= 1 / ¯to6c плюс інтенсивність втрат в процесі обслуговування voбc, при стані S2 ця сумарна інтенсивність подвоюється і т.д. до стану Sп. Після цього стану інтенсивність обслуговування і втрат у процесі обслуговування залишається незмінною, але додається складова, що пов'язана з наявністю втрат "нетерплячих" клієнтів у процесі чекання (vчек), яка пропорційно збільшується по мірі зростання черги очікування до m заявок.
Як слідує з рис.8.7, кількість можливих станів СМО дорівнює (m+n+1) і є обчислюваною величиною. Переходи з будь-якого стану в будь-який інший є можливими, тому в розглянутій СОМ граничний (сталий) режим існує. Використовуючи правило складання системи рівнянь Колмогорова для процесу "загибелі та розмноження", що зображено на рис. 8.7, отримаємо з урахуванням нормовочного рівняння:
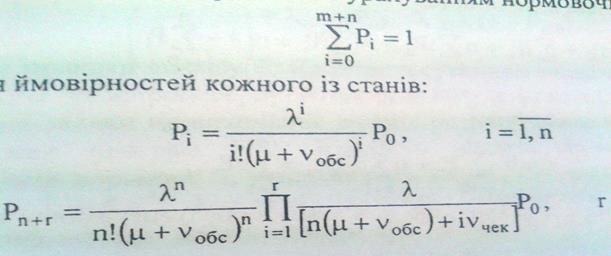
(8.17)
Якщо ввести у розгляд ρ = λ/µ — приведену інтенсивність вхідного потоку, яка дорівнює середній кількості вхідних заявок за час обслуговування однієї заявки, а також aO6c=vO6cV — приведену інтенсивність втрат одного каналу обслуговування і a4eK=v4CK/(x — те ж саме для потоку втрат з черги очікування, то отримаємо
(8.20) (8.21)
При цьому імовірність вільного стану СМО (Ро), що входить в (8.20) і (8.21), визначається за допомогою (8.17) як
Визначимо деякі показники ефективності роботи СМО.
1. Імовірність відмов в обслуговуванні (Рвідм) визначається як імовірність стану СМО коли усі канали обслуговування зайняті і немає вільних місць очікування, тобто при Sn+m
2. Середня кількість каналів (К), зайнятих обслуговуванням. Ця
величина визначається в загальному вигляді як математичне очікування
дискретної випадкової величини К:
К = О-Ро + ІіР1+п|;іРі1+і=ХіР1+/і-Ірі] (8.24)
і=1 і=1 і=0 V і=0 J
3. Середня кількість заявок у черзі очікування (середня довжина
черги) визначається аналогічно:
n jn m
r = 0-XPi+nIrPn+r=£rPn+r (g25)
і=0 г=1 г=1
4. Середня кількість заявок, що пов'язана з обслуговуванням в СМО
5. Середній час очікування заявки у черзі (їчек) і перебування заявки в СМО(їсист):
їчек=?М; Їсист=гД- (8.27)
6. Імовірність втрат в СМО (РВТр) визначається як
| (8.28) |
| Р |
= р + р + Р • втр * відм х п чек х п оос 5
де РПчек. Рцобс.— відповідно імовірності залишання "нетерплячими" заявками черги та залишання ними системи в процесі обслуговування.
Значення Р„Обс визначимо як відношення сумарної інтенсивності залишань заявками системи за час обслуговування, яка дорівнює К -уо6с, до інтенсивності вхідного потоку, тобто
Рпобс=~&- (8-29)
Аналогічно
РПчек=~^ (8-30)
7. Після визначення імовірності втрат (Рвтр) можна визначити
імовірність появи будь-якої заявки, що надійшла до СМО для
обслуговування, в вихідному потоці обслужених заявок (імовірність її
обслуговування Ровс)
Ров.-1-Рир (8.31)
Ця величина чисельно співпадає з відносною пропускною здатністю СМО, яка також характеризує долю вихідних заявок, що буде обслужена, тобто q = РОбс ■
8. Тоді інтенсивність потоку обслужених заявок (вона ж є і
абсолютною пропускною здатністю СМО (А)
д = v_ =p,.^ = wi_p'\ (g 32)
5. Як приклад аналізу СМО із застосуванням вищезазначених формул розглянемо двохпроцесорну обчислювальну систему (ОС), на вхід якої надходять заявки на виконання певних розрахунків за допомогою деяких прикладних програм [13]. Кількість джерел вимог на здійснення розрахунків дорівнює 3, інтенсивність вимог, що надходять від кожного джерела: Л-і = 6 с"1; ^.2=15с"'; Л,3 = 9 с"1. Процесори ОС приймаються однотипними, що мають швидкодію В =50-103 опер/с. Обслуговування кожної заявки (тобто проведення відповідних розрахунків) у середньому потребує виконання 0=2,5-10 операцій, при цьому конкретна кількість операцій, необхідна для виконання кожної заявки, міняється випадковим чином з експоненціальним законом розподілу кількості операцій
Для збереження заявок, що не можуть бути прийнятими до виконання миттєво, виділена буферна зона пам'яті, куди розміщується інформація про чотири заявки. Час перебування заявки в ОС не має перевищувати випадкової величини tuou, що має математичне очікування їдоп=0,1 с і експоненціальний розподіл часу перебування в буфері. Режим обробки інформації — безпріоритетний. Необхідно визначити імовірності усіх станів ОС в граничному (сталому) режимі, а також основні показники її ефективного функціонування.
Перш за все сформулюємо задачу в термінах СМО. Розглядається багатоканальна розімкнута СМО (п=2) з відмовами і обмеженням черги очікування (т=4), з "нетерплячими" заявками з інтенсивністю залишань системи v = v4eK= vo6c= 1 /0,1 =10 с'1. Вхідний потік заявок Х = Х\ + Х2+ Хз = 30 с"1. Потік обслуговування одним процесором (одним каналом) ОС ц = В"/© = 50 • 103/(2,5■ 103 )= 20 с"1.
Визначаємо імовірність вільного стану СМО: Ро=[1+1+0,5+0,5(0,4286+0,1607+0,0536+0,0161)]"1 => Р0=0,3534.
Таким чином, в сталому режимі 35,34% часу роботи ОС буде вільною.
Граничні імовірності інших станів розрахуємо відповідно до (8.20) і (8.21):
Рі=0,3534; Р2=0,1767; — черга відсутня;
Р3=0,0757; Р4=0,0284; Р5=0,0085; Р5=0,0029 — стани СМО при наявності в буфері черги заявок довжиною 1, 2, 3, 4 заявки відповідно .
Середня кількість зайнятих каналів (процесорів)
К = 1 • Р, + 2 • Р2 + 2 ■ (і - Ро - ^ - P2J = 0,9398
Відносне завантаження одного процесора і середня довжина черги дорівнюють відповідно:
Для зручності проведення розрахунків режимів функціонування розімкнених СМО різних типів, їх графи станів та основні розрахункові формули, отримані на підставі рівнянь Колмогорова, і яки характеризують ефективність функціонування СМО, зведені в таблиці 8.1..8.6
Таблиця 8.1
| <== попередня сторінка | | | наступна сторінка ==> |
| Типові графи станів СМО | | | Розрахункові формули для одноканальних розімкнених СМО з відмовами |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |