
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ІІ група
Перед вивченням усного множення двоцифрового числа на одноцифрове розглядають властивість множення суми на число. Дана властивість розкривається на основі конкретної сюжетної задачі: “Дівчинка складала букети. Вона брала 3 білі й 2 червоні квітки. Скільки всього квіток у 7 букетах?”
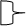 3 біл. кв.
3 біл. кв.
2 черв. кв. 1 букет ? кв. - 7 букетів.
Розв’язати дану задачу можна двома способами:
І спосіб:
1) 3 + 2 = 5 (кв.) – в одному букеті;
2) 5 · 7 = 35 (кв.) – в 7 букетах.
(3 + 2) · 7 = 5 · 7 = 35 (кв.)

ІІ спосіб:
1) 3 · 7 = 21 (кв.) – білих квіток в 7 букетах;
2) 2 · 7 = 14 (кв.) – червоних квіток в 7 букетах;
3) 21 + 14 = 35 (кв.) – разом квіток в 7 букетах.
 (3 · 7) + (2 · 7) = 21 + 14 = 35 (кв.)
(3 · 7) + (2 · 7) = 21 + 14 = 35 (кв.)
Учні пояснюють про що дізнавались кожною дією при розв’язуванні задачі першим і другим способом.
Розв’язавши задачу слід наголосити на виділених виразах, які приводять до висновку:
“Помножити суму на число можна двома способами: 1) обчислити суму й помножити отриманий результат на число; 2) помножити кожний ж доданків на число й скласти отримані результати”.
Закріплення цієї властивості досягається розглядом системи вправ:
1) Знайдіть добутки двома способами: (3 + 7) · 4; (5 + 2) · 3.
2) Розв’яжіть зручним способом: (5 + 7) · 4; (20 + 7) · 3.
3) Знайдіть добутки, обчислюючи спочатку значення виразу в дужках:
(2 + 7) · 4; (3 +6) · 5; (8 + 7) · 3.
Особлива увага звертається на другому способі множення суми на число, адже на цій властивості грунтується прийом множення двоцифрового числа на одноцифрове.
Прийом розглядають за допомогою моделей лічильних одиниць і властивості множення суми на число (двоцифрове число замінюють сумою розрядних доданків). У класі вивішують таблицю:
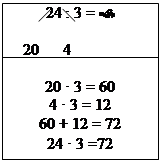 |
Прийом множення одноцифрового числа на двоцифрове розкривають на основі властивості множення числа на суму або на основі переставної властивості множення.
Властивість множення числа на суму є теоретичною основою множення багатоцифрового числа на дво- і трицифрове число.
Дану властивість також розкривають на основі текстової сюжетної задачі: “На змаганнях у першому запливі було 4 човни по 8 спортсменів у кожному. У другому запливі було 3 човни, теж по 8 спортсменів у кожному. Скільки всього спортсменів брали участь у двох запливах?”
| В одному човні | Кількість човнів | Всього спортсменів | |
| І | 8 спортсменів | ? | |
| ІІ |
Розв’язують задачу двома способами:
І спосіб:
1) 4 + 3 = 7 (ч.) – всього човнів;
2) 8 · 7 = 56 (сп.) – всього спортсменів.
8 · (4 + 3) = 8 · 7 = 56 (сп.)
ІІ спосіб:
1) 8 · 4 = 32 (сп.) – спортсменів у 4 човнах;
2) 8 · 3 = 24 (сп.) – спортсменів у 3 човнах;
3) 32 + 24 = 56 (сп.) – всього спортсменів.
8 · 4 + 8 · 3 = 32 + 24 = 56 (сп.)
Учні констатують, що для розв’язування задачі першим способом треба число 8 помножити на суму чисел 4 і 3. За другим способом число 8 множимо окремо на числа 4 і 3. Відповідь однакова – 56 спортсменів. Отже, 8 · (4 + 3) = 8 · 4 + 8 · 3.
На основі цього робиться висновок: “Щоб помножити число на суму використовують два способи: 1) обчислимо суму та помножимо число на отриманий результат; 2) помножимо число на кожний з доданків і складемо отримані результати”.
З опорою на дану властивість розкривають прийом усного множення одноцифрового числа на багатоцифрове. На вивчення цієї теми відводиться два уроки. На першому уроці добуток одно- і двоцифрових чисел учні знаходять, застосовуючи переставну властивість множення. На другому уроці вчаться застосовувати правило множення числа на суму для знаходження такого добутку. Для пояснення використовують таблицю:
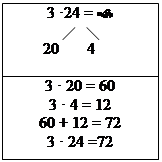 |
Спираючись на таблицю формулюється загальне правило множення одноцифрового числа на двоцифрове: “Щоб помножити одноцифрове число на двоцифрове, потрібно двоцифрове число розкласти на суму розрядних доданків і помножити спочатку число на десятки, а потім на одиниці і одержані добутки додати”.
Випадки усного множення і ділення в межах 1000, які зводяться до табличних або спираються на правило множення суми на число, розглядають у порядку закріплення. До таких випадків належать знаходження значень виразів виду: 70 · 8; 420 : 6; 320 · 3. Наведемо записи кожного виду.
70 · 8 = › 420 : 3 = ›

 7 дес. · 8 = 56 дес. 42 дес. : 6 = 7 дес.
7 дес. · 8 = 56 дес. 42 дес. : 6 = 7 дес.
70 · 8 = 560 420 : 6 = 70
Дані прийоми розглядаються паралельно і зводяться до табличних прийомів множення та ділення.
320 · 3 = (300 + 20) · 3 = 300 · 3 + 20 · 3 = 900 + 60 = 960
У даному випадку використовують властивість множення суми на число.
На наступних уроках розглядається прийом ділення двоцифрового числа на одноцифрове.
Цей прийом грунтується на властивості ділення суми на число. Дану властивість розкривають шляхом розв’язування конкретної сюжетної задачі: “18 червоних і 12 жовтих слив батько поділив порівну між трьома синами. Скільки слив одержав кожний син?”

 18 черв. слив
18 черв. слив
3 синам ? слив – 1
12 жовт. слив
Задачу розв’язують двома способами:
І спосіб:
1) 18 + 12 = 30 (сл.) – всього слив;
2) 30 : 3 = 10 (сл.) – одержав кожний син.
(18 + 12) : 3 =10 (сл.)
ІІ спосіб:
1) 18 : 3 = 6 (сл.) – червоних слив одержав кожний син;
2) 12 : 3 = 4 (сл.) – жовтих слив одержав кожний син;
3) 6 + 4 = 10 (сл.) – всього одержав кожний син.
18 : 3 + 12 : 3 = 6 + 4 = 10 (сл.)
На основі розв’язку даної задачі формулюють правило ділення суми на число: “Поділити суму на число можна двома способами: 1) обчислити суму й поділити отриманий результат на число; 2) кожний з доданків поділити на число й скласти отримані результати”.
Прийом ділення двоцифрового числа на одноцифрове полягає в розкладанні числа на зручні доданки з наступним застосуванням правила ділення суми на число. Учні послідовно розглядають такі випадки ділення: 39 : 3; 72 : 3; 50 : 2.
Враховуючи конкретно-образний характер дитячого сприймання і мислення, дані прийоми доцільно змоделювати лічильними одиницями і на основі записати відповідні алгоритми.
На перших уроках по вивченню даних прийомів добирають такі приклади на ділення, коли число, яке ділиться, розкладалося на розрядні доданки і при діленні їх на число використовувалися б табличні випадки ділення.
Наприклад:
39 : 3 = ›
 |  |
30 9
 |
30 : 3 = 10
9 : 3 = 3
10 + 3 = 13
39 : 3 = 13
Формулюють правило: “Щоб поділити двоцифрове число на одноцифрове, потрібно окремо поділити десятки і одиниці на це число і отримані частки додати”.
Пізніше розглядаються приклади на ділення, де розглянутий вище прийом застосовувати не можна: 56 : 4; 72 : 3; 78 : 6 та ін.
Вказані випадки ділення також грунтуються на властивості ділення суми на число і вимагають моделювання. “Зручність” доданків виявляється в тому, що при діленні першого доданка дістаємо десятки, а при діленні другого – одиниці.
72 : 4 = ›
 |  |
40 32
 |
40 : 4 = 10
32 : 4 = 8
10 + 8 = 18
72 : 4 = 18
Формулюють правило: “Щоб поділити двоцифрове число на одноцифрове, потрібно двоцифрове число замінити сумою зручних доданків, з яких перший є результатом найбільшого табличного множення на дільник, після чого ділять кожен з доданків на число і одержані частки додають”.
За даним правилом розв’язують інші приклади:
72 : 3 = (60 + 12) : 3 = 20 + 4 = 24
78 : 6 = (60 + 18) : 6 = 10 + 3 = 13
50 : 2 = (20 + 20 + 10) : 2 = (40 + 10) : 2 = 20 + 5 = 25
Зразок ділення двоцифрового числа на одноцифрове служить і при діленні круглих трицифрових чисел. Це здійснюється переходом до ділення десятків.
 360 : 3 = ›
360 : 3 = ›
36 дес. : 3 = 12 дес.
| <== попередня сторінка | | | наступна сторінка ==> |
| Що дістаємо в частці від ділення числа на 1? Що дістаємо в частці від ділення числа на самого себе? Наведіть власні приклади ділення на 1 і ділення числа на самого себе. | | | ІІІ група |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |