ІV група

З дією ділення з остачею часто доводиться зустрічатися в практичній діяльності.

На ділення з остачею в межах табличного ділення відводять 3 години. На першому уроці перед поясненням ділення з остачею треба показати, що не завжди можна поділити ту чи іншу кількість предметів порівну.

Зміст дії ділення з остачею розкривається з опорою на зміст дії ділення на вміщення шляхом розгляду конкретної задачі: “20 олівців дівчинка розклала в склянки по 6 олівців в кожній. Скільки потрібно було склянок? Скільки олівців залишилося?”

Задачу ілюструють шляхом виконання маніпуляцій.

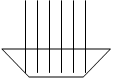Резаультат розв’язання задачі записують у вигляді дії, зразок якої подає вчитель:

20 : 6 = 3 (ост. 2)

ол.ол. скл. ол.

Відповідь: 3 склянки і два олівці.

Дію читають так: 20 поділити по 6 дорівнює 3 і остача 2.

При цьому пояснюють зміст чисел 3 і 2.

Попередньо повторюються назви компонентів при діленні та два види ділення, способи читання кожного виду ділення і вводять назву результату при діленні – частка і остача. При цьому наголошують, що в попередніх випадках ділення можна також говорити про частку і остачу, але остача була рівна нулю, тому на неї не звертали увагу. Тепер остача відмінна від нуля, а тому нею нехтувати не слід. Оскільки дія мала зміст ділення на вміщення, то остача має таке найменування, як ділене і дільник, а частка зовсім інше найменування.

На початкових етапах розглядаються приклади, в яких виконується ділення двоцифрового числа на одноцифрове з остачею.

Хоча прийоми розглядаються в межах табличних прийомів ділення, однак учні зазнають труднощів у доборі цифри частки. Для того, щоб усунути ці труднощі, слід розглянути систему вправ, в яких проілюструвати характер дії і зробити висновки.

13 : 3

13 : 3 = 4 (ост. 1)

12 < 13, 12 : 3 = 4, 13 – 12 = 1

частка остача

міркування при виконанні дій є такими: спочатку визначаємо число, яке найближче до діленого без остачі на дільник (12 < 13). Потім ділимо це число на дільник і знаходимо частку (12 : 3 = 4). Від діленого віднімаємо число, яке ділили, одержана різниця є остачею.

Далі учні самостійно виконують приклади на ділення з остачею і закріплюють алгоритм виконання дій.

15 : 4

12 < 15; 12 : 4 = 3; 5 – 12 = 3; 15 : 4 = 3 (ост.3)

частка остача

17 : 6

12 < 17; 12 : 6 = 2; 17 – 12 = 5; 17 : 6 = 2 (ост. 5).

частка остача

Аналізуючи систему прикладів увагу учнів звертаємо на:

1) добирати слід число, яке ділиться на дільник без остачі, серед чисел менших від діленого;

2) частку при діленні знаходять як результат табличного ділення цього числа на дільник;

3) остача, яка є різницею діленого і числа, що ділиться, завжди менша від дільника.

<== попередня сторінка	\|	наступна сторінка ==>
ІІІ група	\|	Останнє положення учні засвоюють з труднощами і часто невірно знаходять остачу.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.043 сек.