
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Критерій вірогідності різниці двох середніх значень (критерій Стьюдента)
Однією з важливих задач біологічного дослідження є отримання даних про результати дії зовнішніх факторів на живий об’єкт. Для проведення дослідів вибираються дві групи об’єктів (не обов’язково однієї чисельності), одна з яких є піддослідною, а інша – контрольною.
Наприклад, необхідно виявити ефективність застосування деякого препарату, що має метою підвищення опору організму по відношенню до конкретної інфекції.
Дослід може бути поставлений так: беруть дві групи тварин. Тваринам однієї групи препарат вводять, а іншим – не вводять. Перша група буде піддослідною, а друга – контрольною. Потім тваринам обох груп вводять інфекцію і спостерігають, скільки днів переживуть тварини піддослідної групи і контрольної.
У таблиці зведені результати досліду:
| Число днів | n | M | 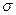
| m | |||||||
| Дослід | 6,25 | 1,25 | 0,22 | ||||||||
| Контроль | 5,22 | 0,97 | 0,2 |
З таблиці видно, що середні значення для піддослідної і контрольної груп не співпадають. Але це недостатньо для доведення ефективності препарату.
Насправді, кожна група тварин є випадковою вибіркою з генеральної сукупності. Та , як відомо, для різних вибірок, отриманих з однієї і тієї ж генеральної сукупності, середні арифметичні будуть різними.
Покажемо це на простому прикладі.
Нехай є генеральна сукупність, яка складається з 5 варіант (N=5).
xi : 8, 16, 20, 24, 32.
(Числа можуть позначати висоту рослин у сантиметрах).
Замінимо вивчення усієї генеральної сукупності вивченням вибірок з неї об’ємом n=4. Ось ці вибірки: 1) 8, 16, 20, 24;
2) 8, 16, 20, 32;
3) 8, 16, 24, 32;
4) 8, 20, 24, 32;
5) 16, 20, 24, 32.
Обчислюючи для кожної вибірки середнє арифметичне, отримуємо такі значення: М1=17, М2=19, М3=20, М4=21, М5=23.)
Тому виникає питання: чи вважати розбіжність між середніми значеннями в піддослідній і контрольній групах просто розбіжністю між двома вибірковими середніми, чи ця розбіжність обумовлена ефективною дією препарату? Або, інакше кажучи, чи можливо узагальнити висновок про ефективність препарату і розглядати вибірки піддослідної і контрольної груп, як вибірки з різних генеральних сукупностей?
Таке питання відноситься до проблем вірогідності різниці середніх арифметичних.
Розглянемо загальний метод розв’язання цієї проблеми.
Починають з припущення, що обидві вибірки зроблені з однієї генеральної сукупності. Тоді різниця між вибірковими середніми пояснюється існуванням такої різниці взагалі. Таке припущення називають нульовою гіпотезою і позначають Н0.
Далі обчислюють ймовірність того, що при умові правильності нульової гіпотези, розбіжність між вибірковими середніми (М1 – М2) може досягти тієї величини, яка є. Якщо ця ймовірність виявиться малою, то нульова гіпотеза відкидається. Граничне допустиме значення ймовірності називають рівнем значущості і позначають a . Яке ж значення ймовірності вважати малим? Як правило, вибирають одне з таких значень a = 0,05 = 5 %, a = 0,01 = 1 %, a = 0,001 = 0,1 %. Різниця між вибірковими середніми вважається значущою (тобто, реальною), якщо ймовірність правильності нульової гіпотези менша за рівень значущості. У такому разі нульова гіпотеза відкидається.
Вибір того чи іншого конкретного значення a визначається конкретними задачами дослідника. Наприклад, якщо досліджується новий лікарський засіб і треба довести його нешкідливість для життя, то навіть рівень значущості 0,001 буде зависоким. Навпаки, якщо мова йде про підвищення продуктивності стада за рахунок недорогої зміни раціону, то достатньо і невеликої впевненості у позитивному результаті.
Критерій, який дозволяє визначити вірогідність різниці вибіркових середніх, був сформульований англійським математиком Вільямом Госсетом ( 1876 – 1937), який працював під псевдонімом Стьюдента. Критерій носить назву критерію Стьюдента.
Згідно з ним обчислюється величина t = 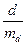 , яка потім порівнюється з табличною величиною tst.
, яка потім порівнюється з табличною величиною tst.
Чисельник d – різниця між середніми арифметичними двох вибіркових груп ( знак різниці значення не має: d = | М1 –М2|), md = 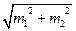 - помилка вибіркової різниці; m1,m2 – помилки репрезентативності порівнюваних вибіркових середніх (m1 =
- помилка вибіркової різниці; m1,m2 – помилки репрезентативності порівнюваних вибіркових середніх (m1 = 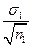 , m2 =
, m2 = 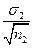 ,
, 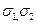 - середні квадратичні відхилення відповідних вибірок, n1, n2 – об’єми вибірок).
- середні квадратичні відхилення відповідних вибірок, n1, n2 – об’єми вибірок).
За таблицею 1 визначається значення tst, яке залежить від двох параметрів:
величини n = n1+n2-2 (n називається числом степенів волі) і ймовірності Р=1-a (ймовірність впевненості у неправильності нульової гіпотези).
Якщо t £ tst, то нульова гіпотеза приймається ( згідно прикладу це означає, що препарат не ефективний). Якщо ж t > tst, то Н0 відкидається.
Приклад 4.
За даними прикладу 3 , оцінимо ефективність препарату, використовуючи критерій Стьюдента. Гіпотеза Н0: препарат не ефективний.
Середнє арифметичне значення кількості днів, які пережили тварини піддослідної групи М1 = 6,25, а контрольної М2 = 5,22. Кількість тварин піддослідної групи (об’єм вибірки) n1 = 32, а контрольної n2= 23. Середні квадратичні відхилення s1 =1,25, s2 = 0,97. Помилки репрезентативності:
m1 =0,22, m2 = 0,2. Отже, згідно критерію Стьюдента обчислюємо величину t = 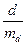 , де d = | М1 –М2| = | 6,25 – 5,22 | = 1,03; md =
, де d = | М1 –М2| = | 6,25 – 5,22 | = 1,03; md = 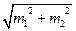 = =
= = 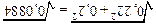 »0,297.
»0,297.
t = 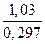 »3,47.
»3,47.
За таблицею 1 визначимо значення величини tst . Число степенів волі
n = n1 + n2 – 2=32+23 -2= 53»50.
При різних рівнях значущості, маємо t 0,05 = 2,01; t 0,01 = 2,68; t 0,001 = 3,5.
Так як t > t 0,01, то нульова гіпотеза відкидається з ймовірністю 0,99.
Висновок: препарат можна вважати ефективним у 99%.
| <== попередня сторінка | | | наступна сторінка ==> |
| Помилка вибіркової середньої арифметичної | | | Метод j (фі) |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |