Види взаємозв'язків між явищами

Непараметричні методи виявлення та вимірювання зв'язків.

Основи кореляційно-регреасійного аналізу.

Дисперсійний анализ.

Метод аналітичного групування.

Види взаємозв'язків між явищами.

План лекції

ВИМІРЮВАННЯ ВЗАЄМОЗВ'ЯЗКІВ

ТЕМА 7. СТАТИСТИЧНІ МЕТОДИ

Одним iз найзагальніших законів об'єктивного світу є закон загального зв'язку i залежності між явищами суспільного життя. Усі явища суспільного життя існують не ізольовано, а у нерозривному взаємозв'язку, тобто залежать одне від одного, тому вивчення будь-якого явища буде неповним, якщо не досліджені його зв'язки з іншими явищами i процесами. Статистичне дослідження взаємозв'язків дає можливість виявити не тільки наянівсть i напрямок зв'язку, але дозволяє кількісно оцінити i виразити його аналітично.

Визначення зв'язків між явищами дає змогу перейти від констатації фактів до пояснення i використання їx на практиці. Так, при вивченні урожайності сільськогосподарських культур можна визначити кількісні характеристики виливу багатьох фактopiв на урожайність. Це дозволяє виявити резерви зростання урожайності, встановити ступінь залежності їx як від об'єктивних причин, так i від умов діяльності сільськогосподарських підприємств. Визначення взаємозв'язків дозволяє проводити науково обгрунтовані прогнози.

Зв'язки між явищами, окремими їх ознаками досить різноманітні, однак у будь-якому випадку одні ознаки виступають як фактори, що впливають на інші i зумовлюють їx зміну, інші — як результати дії цих факторів. Одні iз них є причиною, інші наслідком.

Якщо перші прийнято називати ознаками-факторами, або факторними (причинними) ознаками, то другі — результативними (наслідковими) ознаками.

Різноманітністъ зв'язків, в яких перебувають явища, зумовлює необхідність їx класифікації, зведення зв'язків до певних типів, форм за їx істотними рисами i властивостями.

В основу класифікації зв'язків у статистиці покладено відмінність i подібність зв'язків за такими їx особливостями, як ступінь тісноти, спрямованість, аналітичне вираження, одиничність або множинність факторів. Відповідно до цього розрізняють зв'язки функціональні i кореляційні, прямі i обернені, прямолінійні i криволінійні, однофакторні i багатофакторні.

За статистичною природою зв'язки поділяють на функциональні i стохастичні. При функціональному зв'язку кожному можливому значенню факторної ознаки х відповідає чітко визначене значення результативної ознаки —у, тобто функціональні зв'язки характеризуются повною відповідністю між причиною i наслідком, факторною i результативною ознаками. Така залежність притаманна фізичним, хімічним явищам тощо. У суспільних процесах це найчастіше зв'язок складових елементів розрахункових формул відповідних показників, наприклад, залежністъ валового збору від урожайності сільськогосподарської культури i розміру посівної площі.

На відміну від функціональних, стохастичні зв'язки неоднозначні. Стохастичні зв'язки проявляються як узгодженість варіації двох чи бшьше ознак. У ланці зв'язку "х→у" кожному значенню ознаки х відповідає певна множина значень ознаки у, які утворюють так званий умовний розподіл. Стохастичний зв'язок, відбиваючи множинність причин i наслідків, виявляється в зміні умовних розподлів.

Якщо умовні розподіли замінюються одним параметром — середньою 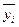, то такий зв'язок називають кореляційним. Отже, кореляційний зв'язок є різновидом стохастичного i виявляється в зміні середніх умовних розподілів, що схематично ілюструструє табл. 10.1.

За напрямком дії (спрямованістю) розрізняють зв'язок прямий i обернений. Прямий — це такий зв'язок, при якому зі збільшенням або зменшенням значень факторної ознаки відповідно збільшуєгься або зменшується значення результативної ознаки, тобто факторна i результативна ознаки змюнюються в одному напрямку.

Таблиця 10,1. Види взаємозв'язків

Факторна ознака, X_і	Результативна ознака у при наявності зв'язку:
функціонального	стохастичного	кореляційного
X₁ X₂ Х₃ _… Xn	У₁ У₂ У₃ _… Уn	У₁У₂ У₁У₂У₃ У₂У₃У₄ … Уn_-1Уn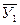

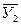
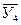
Прикладом прямого зв'язку може бути зв'язок між фондоозброєністю i продуктивністю праці, між собівартістю продукції i рівнем рентабельності.

Оберненим зв'язком називають такий, при якому значення результативної ознаки змінюєтъся в протилежному напрямку відносно зміни значення факторної ознаки. Прикладом такого зв'язку може бути продуктивність праці i собівартість продукції.

Слід мати на увазі, що прямий i обернений зв'язки можуть переходити один в інший. Так, прямий зв'язок після досягнення факторною ознакою певного рівня в деяких випадках себе вичерпує i потім робиться оберненим, тобто з наступним збільшенням значення факторної ознаки значення результативної ознаки зменшується.

За формою аналітичного вираження в загальній класифікації виділяють зв'язки прямолінійні та криволінійні. .Якщо певний зв'язок явищ можна точно або наближено зобразити рівнянням будь-якої прямої лінії, то його називають лінійним (прямолінійним) зв'язком, а якщо рівнянням будь-якої кривої лінії (параболи, гіперболи i т.п.) — нелінійним (криволінійним).

Аналітичним рівнянням можна описувати лише функціональні зв'язки.і Кореляційні зв'язки описуються рівнянням лише наближено. Однак, навіть наближене описування за допомогою аналітичних рівнянь корелящйних зв'язків суспільних явищ дає можливість отримати результати, цілком придатні для наукових i практичних потреб.

Для відповіді на питания про наявність або відсутність кореляційного зв'язку використовують ряд специфічних методів:

• елементарні прийоми (паралельне порівняння рядів значень факторної i результативної ознак, балансовий метод, графічне зображення, метод аналітичного групування);

• дисперсійний аналіз;

• кореляційно-регресійний аналіз.

<== попередня сторінка	\|	наступна сторінка ==>
Контрольні запитання і завдання	\|	Метод аналогичного групування

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.