• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Призма.

Многогранники.

Тілом називається множина точок простору яке складається із обмеженої області та її межі.

Многогранники – це тіло, поверхня якого складається із скінченої кількості плоских многогранників.

Площина многогранника називається його гранню. Сторони граней називаються ребрами многогранника, вершини – вершинами многогранника.

Опуклим многогранник називається правильним, якщо його грані є правильними многогранниками з однією і тією самою кількістю сторін, а в кожній вершині сходиться одне і те ж число ребер.

Існує чотири типи правильних опуклих многогранників:

1. Куб (всі грані квадрати, у кожній вершині сходиться по три ребра);

2. Октаедр (грані правильні трикутники, у кожній вершині сходиться по чотири ребра);

3. Дедекаедр (грані правильні п’ятикутники, у кожній вершині сходиться по три ребра);

4. Ікосаедр (грані правильні трикутники, у кожній вершині сходяться по п’ять ребер).

3. Поняття про об’єми та площі поверхні тіл.

Для простих тіл об’єм – додатна величина, числове значення якої має такі властивості:

1. Рівні тіла мають рівні об’єми.

2. Якщо тіло розбито на частини, які є простими тілами, то об’єм цього дорівнює сумі об’ємів його частин.

3. Об’єм куба, ребро якого дорівнює одиниці довжини, дорівнює 1. Площа поверхні многогранника є сума площ всіх його граней.

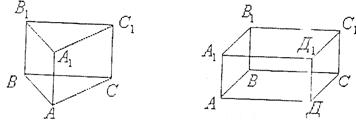
Призма називається многогранник, який складається з двох плоских многогранників, які лежать у різних площинах і суміщаються паралельними перенесеннями, та всіх відрізків, що сполучають відповідні точки цих многогранників.

Многогранники називаються основами призми. Відрізки, що сполучають відповідно вершини – бічними ребрами призми. Основи призми лежать у паралельних площинах і рівні. Бічні ребра призми паралельні і рівні. Поверхня призми складається з основ і бічної поверхні. Висотою призми називається відстань між площинами її основ. Відрізок, що сполучає дві вершини призми, що не належать одній грані, називається діагоналлю призми. Призма називається прямою, якщо її бічні ребра перпендикулярні до основ. Пряма призми називається правильною, якщо її основи є правильними многокутниками. Призма, в основі якої лежить паралелограм називається паралелепіпедом. Прямий паралелепіпед, у якого основа є прямокутник, називається прямокутним паралелепіпедом.

Властивості паралелепіпеда:

Теорема 1. Протилежні грані паралелепіпеда паралельні і рівні.

Теорема 2. Діагоналі паралелепіпеда перетинаються в одній точці і діляться пополам.

Теорема 3. У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів трьох вимірів.

Теорема. Бічна поверхня прямої призми дорівнює добутку основи на висоту призми.

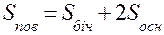
Теорема. Об’єм призми дорівнює добутку площі основи на висоту.

5. Піраміда.

Пірамідою називається многогранник, який складається з плоского многогранника – основи піраміди, точки, які не лежать у площині основи – вершини піраміди і всіх відрізків, що сполучають вершину піраміди з точками основи.

Відрізки, що сполучають вершину піраміди з вершинами основи, називаються бічними ребрами.

Висотою піраміди називається перпендикуляр, опущений з вершини піраміди на площину основи.

Піраміда називається правильною, якщо в її основі лежить правильний многокутник і вершина проектується в його центр. Висота бічної грані правильної піраміди називається апофемою піраміди.

Теорема 1. Бічна поверхня правильної піраміди дорівнює півпериметра основи на апофему.

Теорема 2. Об’єм піраміди дорівнює добутку площі основи на третину висоти.

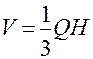
6. Зрізана піраміда.

Теорема 1. Площа, яка паралельна основі піраміди й перетинає її, відтинає подібну піраміду.

Друга частина піраміди називається зрізаною пірамідою.

Теорема 2. Бічна поверхня правильної зрізаної піраміди дорівнює добутку півсуми периметрів основ на апофему.

Теорема 3. Об’єм зрізаної піраміди:

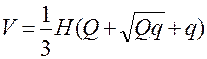
7. Циліндр.

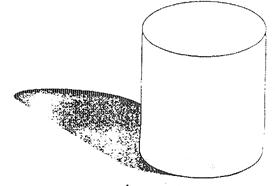
Циліндром називається тіло, утворене при обертанні прямокутника навколо однієї з його сторін.

Основи циліндра – круг.

Відрізки, що сполучають точки кіл – твірні циліндра.

Радіус циліндра – це радіус його основи.

Висота циліндра – це відстань між площинами основ.

Теорема 1. Площа бічної поверхні циліндра дорівнює добутку довжини кола основи на висоту.

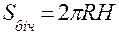
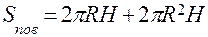
Теорема 2. Об’єм циліндра дорівнює добутку площі основи на висоту.

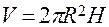
Читайте також:

1. Малюнок № 7.6. Трикутна призма.

Переглядів: 1229