
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Кристалографічні параметри Вейса та індекси площин Міллера. Міжплощинні відстані
Із наведеного вище закону Гаюі очевидно, що серію відношень раціональних чисел для всіх паралельних площин можна представити як відношення цілих взаємно простих чисел p; q; r – параметри Вейса.
В кристалографії прийнято характеризувати площини (або нормалі до них) не параметри, а індексами Міллера. Індекси Міллера – це величини, зворотні параметрам Вейса, приведені до цілих чисел.
Подвійні відношення параметрів одиничної грані до даної грані:
p / mp : q / nq : r / sr = l / m : l / n : l / s = h : k : l
Тоді (hkl) – символи істинної (даної) грані.
Тобто, h, k, l – індекси символу грані, індекси Міллера.
Рисунок 1.10 ілюструє порядок визначення індексів Міллера для компланарних площин з параметрами Вейса:
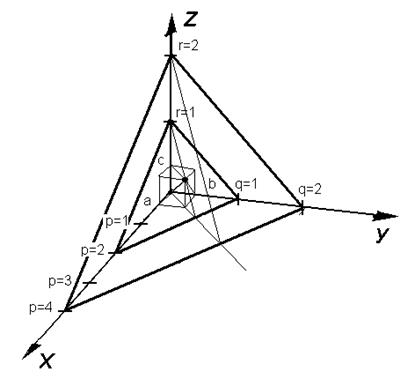
| Площина №1:
p = 2; q = 1; r = 1
Індекси Міллера: 1 / 2 : 1 / 1 : 1 / 1 = 1, 2, 2
Площина №2:
p = 4; q = 2; r = 2
Індекси Міллера: 1 / 4 : 1 / 2 : 1 / 2 = 1, 2, 2
Площина №3:
p = 6; q = 3; r = 3
Індекси Міллера: 1 / 6 : 1 / 3 : 1 / 3 = 1, 2, 2
і т.д.
У загальному вигляді знаходження індексів Міллера:
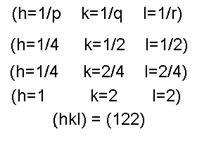
|
| Рисунок 1.10 – Кристалографічні індекси площин |
Тобто, всі площини цієї 1-ої, 2-ої, 3-ої і т.д.. n-ої трансляції завжди будуть мати одні й ті ж самі індекси Міллера, тому вони складають у розглянутому прикладі сімейство площин (122), або в загальному вигляді – (hkl).
Ребра кристалу відповідають рядам гратки (див. рис. 1.3 б), а грані площинам сітки (див. рис. 1.3 а) з найвищою ретикулярною щільністю.
Тому, наявність цілих чисел в законі Гаюі пояснюється тим, що пласкі сітки збігаються з вузлами рядів. Наявність малих чисел пов’язана з тим, що гранню кристалу є не аби яка пласка сітка, а тільки сітка густо всаджена матеріальними частками (ретикулярно щільна).
Кожне сімейство площин з індексами (hkl) характеризується своєю міжплощинною відстанню «d», тобто, відстань між двома сусідніми паралельними площинами (dhkl – в загальному вигляді), наприклад – d010 на рис. 1.11 а.
Всі кристалографічно ідентичні сімейства площин, тобто, сімейства площин з однаковою міжплощинною відстанню, утворюють сукупність площин {hkl}.
Розрахунок міжплощинної відстані виконується за формулами що пов’язують індекси відповідної площини та параметри (періоди) гратки. Наприклад, для кубічної гратки відповідні розрахункові формули:
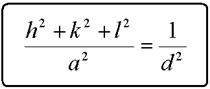
| 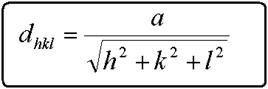
|
| <== попередня сторінка | | | наступна сторінка ==> |
| Закони геометричної кристалографії | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |