Рівняння руху субстанції

Для одержання рівнянь руху (зміни) будь-якої субстанції використовуємо метод фіксованої крапки простору. Застосовуючи його ми описуємо характеристики потоку субстанції в нерухливій крапці, спостерігаючи рух нескінченно малого обсягу субстанції. Швидкості зміни розглянутих функцій f(x,y,z,t) визначаються субстанціональної похідній. Тому що всі зміни можуть відбуватися тільки при наявності інерційного впливу субстанції, що рухається, приймемо його кількісним заходом, за аналогією з інертною масою, інертну субстанцію 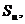у припущенні, що відомий еквівалент між її величиною й масою, що забезпечує вплив.

У якості вихідного, запишемо рівняння субстанціональної похідної для імпульсу інертної субстанції і її щільності.

Для субстанції:

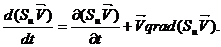(20)

Для щільності субстанції:

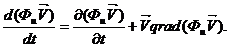(21)

Для одержання диференціального рівняння руху (зміни) будь-якої субстанції необхідно підставити в загальне рівняння інерційного впливу величину даної субстанції або її щільності.

Розглянемо, як приклад, окремий випадок переносу імпульсу в механіку, для якого 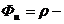щільність. Підставимо дану величину в рівняння (21):

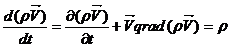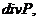g+ (22)

де 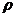g – щільність масових сил, у якості яких розглядаються тільки сили ваги; g – сила ваги, що доводиться на одиницю маси, визначається її прискоренням: 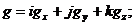- тензор напруги поверхневих сил.

Рівняння (22), придатне для всіх суцільних середовищ, може бути записане у вигляді:

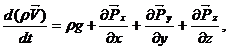(23)

де 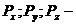вектори поверхневих сил, прикладені до майданчиків, нормальних до осей координат: x, y, z.

Суми щільності масових і поверхневих сил, що діють на елементарну частку, можна виразити в проекціях на осі координат x,y,z у такий спосіб:

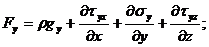
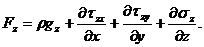(24)

Рівняння (24) можна записати в проекціях у вигляді:

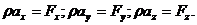(25)

Помноживши ці значення на обсяг елементарної частки 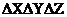, одержимо вираження другого закону Ньютона для напрямків осей координат:

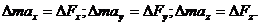(26)

Рівняння (24) – (26) є фундаментальними механіки суцільних середовищ.

Якщо в обсязі, що рухається, величина імпульсу субстанції: 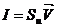залишається постійної, то це означає, що обсяг повністю ізольований і кількість вхідної й вихідної субстанції буде однаково. Рівняння (20), (21) переносу (зміни) імпульсу субстанції в цьому випадку будуть називатися рівняннями збереження імпульсу субстанції.

Для субстанції:

(27)

Для щільності субстанції:

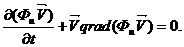(28)

Рівняння збереження імпульсу субстанції являє собою баланс впливів: активного інерційного впливу 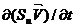потоку субстанції на середовище й опору середовища 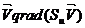переходу в інший стан, який характеризується швидкостями зміни потоку по напрямках руху. Рівняння (27), (28) виражають закон збереження, що є загальним для всієї фізики. Баланс інерційного впливу й опору йому виражає фізичну сутність процесу існування всього живого й неживого в природі.

Для стаціонарних процесів, що встановилися, коли величина імпульсу субстанції не залежить від часу, рівняння збереження (27) буде

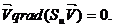(29)

<== попередня сторінка	\|	наступна сторінка ==>
Рівняння збереження субстанції	\|	Фізичні передумови єдиної теорії

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.014 сек.