• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Сили тиску рідини на плоскі поверхні.

Визначення сили тиску рідини, що діє на ту або іншу поверхню, має велике практичне значення при механічних розрахунках стінок, заглушок, перегородок, мембран та інших пристроїв.

Доведення питання про силу тиску рідини на плоску стінку зручніше проводити в координатних осях, одна з яких спрямована уздовж стінки.

Почнемо з більш загального випадку – визначення сили тиску рідини на плоску поверхню (рис. 6), яка нахилена до обрію під кутом α, і яка має площу F.

Нехай вільна поверхня знаходиться під впливом надлишкового тиску р_м, який може бути виражений відповідною п’єзометричною висотою . Тому становить інтерес тільки сила надлишкового тиску.

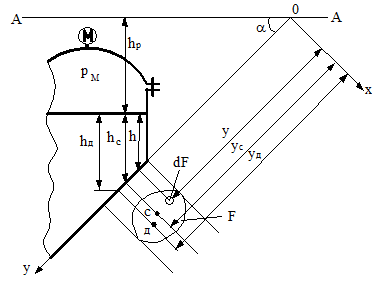
Рис. 6 Визначення сили тиску рідини на плоску поверхню.

За ось координат у приймемо лінію, яка збігається з напрямком плоскої стінки, і продовжимо цю лінію до перетинання з п’єзометричною площиною A-A у точці О. З точки О проведемо ось Ox, яка є нормальною до поверхні стінки. Для зручності розгляду стінку повернемо навколо осі Oy до з’єднання з площиною креслення. Тоді на площині побачимо фігуру в натуральну величину. Визначимо величину сили тиску рідини на стінку. Відзначимо, що на різні точки площі F, що знаходяться на різних глибинах, діють відповідно до основного рівняння гідростатики різні тиски. Знайдемо силу тиску на елементарну площадку. При цьому відстань елементарної площадки dF від осі Ox буде дорівнювати y. Надлишковий гідростатичний тиск в області площадки dF може бути прийнятий рівним . Тоді елементарна сила dР визначиться:

,

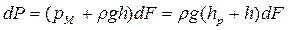де – відстань по вертикалі від даної точки до п’єзометричної площини A-A. З рис. 6 видно, що 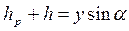. Отже, елементарна сила тиску буде:

Читайте також:

1. Аеровані промивальні рідини
2. Взаємозв’язок характеристик порід, визначених при статичному і динамічному втискуванні
3. Вибір схеми підключення абонентів залежно від режимів тиску.
4. Види течії в’язкої рідини
5. Види тиску.
6. Визначення зусилля попереднього обтиску і величини попереднього напруження
7. Визначення показників механічних властивостей гірських порід методом статичного втискування штампа
8. Визначення ударного тиску.
9. Вимір артеріального тиску.
10. Вимірювання витрат за перепадом тиску
11. Вимірювання витрати за перепадом тиску
12. Вимірювання механічних сил та тиску

Переглядів: 6306