• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

IНТЕГРАЛ ДЮАМЕЛЯ

ЗА ДОПОМОГОЮ ПЕРЕХIДНОЇ ХАРАКТЕРИСТИКИ.

ВИЗНАЧЕННЯ ВIДГУКУ КОЛА НА СКЛАДНУ ДIЮ

Припустимо, що зовнiшня дiя задана у виглядi функцiї 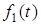(рис.7.1а). Задану неперервну дiю при можна подати як суму початкового "стрибка" (ступінчастої дiї) та множини нескiнченно малих "сходинок" 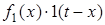, якi послiдовно змiщуються за часом на iнтервал 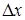. Цi елементарнi дiї продовжуються обов'язково до +¥, хоча можуть починатися у рiзнi моменти часу i мати рiзну висоту (рис.7.1б). Одну з таких елементарних дiй вiдмiчено на рис.7.1 штрихуванням. Таке подання функцiї 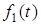буде точним, якщо 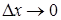, (n - кiлькiсть "стрибкiв").

а) б)

Рисунок 7.1

Згiдно з визначенням похiдної, знайдемо величину будь-якого малого стрибка:

;

;

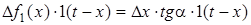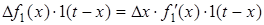або, здiйснюючи граничний перехiд,

.

Знайдемо значення реакцiї кола у деякий момент часу . Ступінчаста дiя до моменту t обумовлює реакцiю , де - перехiдна характеристика. Аналогiчно, дiї вiдповiдає вiдгук , або пiсля граничного переходу

.

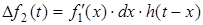Якщо коло є лiнiйним, до нього можна застосувати принцип суперпозицiї. Тодi вiдгук кола можна визначити як суму елементарних вiдгукiв

.

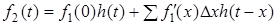Вважаючи, що кожний стрибок на входi нескiнченно малий (тобто 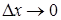, і сума переходить до iнтеграла), отримуємо:

. (7.1)

Вираз (7.1) має назву iнтеграла Дюамеля. В iнтегралi Дюамеля значення вiдгуку залежить вiд моменту спостереження.

Iснує кiлька форм iнтеграла Дюамеля. Рiзнi форми застосовують для рiзних вхiдних дiй. Так, якщо ввести нову змiнну 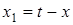, тo

,

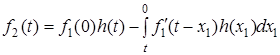або пiсля змiни порядку iнтегрування i повернення до попереднього позначення x для змiнної, за якою проводиться iнтегрування, матимемо

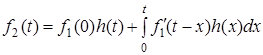. (7.2)

Розглянемо приклад. Нехай до кола, яке складається з послiдовно з’єднаних опору та ємностi, увімкнено напругу

.

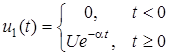Треба знайти спад напруги на опорi.

Класичний метод у цьому випадку дає громiздке рiшення. Вiн є ефективним, якщо вхiдна дiя незмiнна за часом або змiнюється за синусоїдним законом. При iнших типах дiї складно визначити вимушену складову. Тому зручнiше скористатись iнтегралом Дюамеля.

Отже, скористаємось формулою (7.1). Для цього попередньо визначимо величини, якi входять до неї:

; ; ;

; .

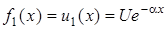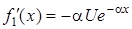Пiдставивши цi значення до (7.1), матимемо

.

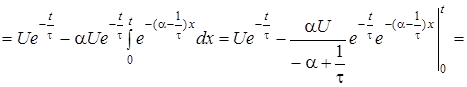
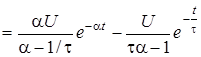Вигляд графiка вiдгуку 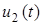залежить вiд значень i 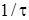(рис.7.2):

1) якщо t =1 мкс, a =0,5 мкс^-1, тодi ;

2) якщо t = 1 мкс, a = 2 мкс^-1, то .

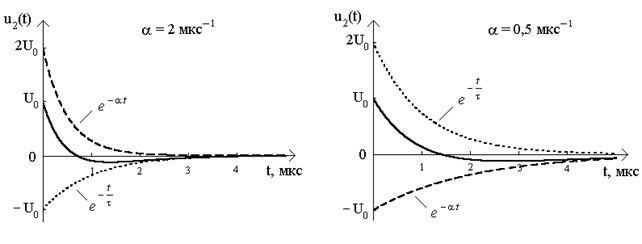
а) б)

Рисунок 7.2

7.1 Визначення вiдгуку кола на складну дiю, яка має

розриви першого роду

У спiввiдношеннях (7.1) - (7.2) функцiя 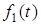є неперервною функцiєю за часом. У тому випадку, коли 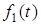є шматково-неперервною функцiєю, у формулах слiд враховувати iснування додаткових, окрiм точки 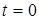, розривiв першого роду, що еквiвалентне iснуванню додаткових ступінчастих дiй. (Нагадаємо, що розрив першого роду - це порушення неперервностi, при якому iснують границi функцiї у точцi розриву лiворуч i праворуч). Реакцiя на кожну з цих додаткових ступінчастих дiй знаходиться за формулою

, (7.3)

де 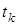- k-та точка розриву неперервностi функцiї .

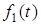Вигляд вiдгуку, який розраховується за допомогою iнтеграла Дюамеля, залежить вiд моменту спостереження t. Для функцiї, зображеної на рис.7.3а, маємо три моменти спостереження.

1. . При цьому діють нескiнченно-подовженi "стрибки" до моменту t (рис.7.3б). Тодi

.

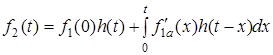2. (рис.7.3в).

.

3. .

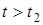Кожна з отриманих формул справедлива для свого iнтервалу часу.

а) в)

б) г)

Рисунок 7.3

7.2 Визначення вiдгуку кола на складну дiю за допомогою iмпульсної

характеристики. Iнтеграл накладання

Реакцiю кола на довiльну дiю можна визначити також за допомогою iмпульсної характеристики. Представимо дiю 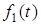у виглядi суми елементарних вiдеоiмпульсiв прямокутної форми та нескiнченно малої тривалостi. Одну з таких iмпульсних дiй, яку прикладено у момент x, позначено на рис.7.3г. Вона характеризується тривалiстю dx i висотою 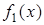. Нескiнченно мала складова реакцiї, яка обумовлена цiєю дiєю, складе 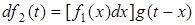, оскiльки площа iмпульсної дiї дорiвнює .

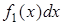У вiдповiдностi з принципом накладання повна реакцiя кола у момент t дорiвнюватиме сумi нескiнченно великої кiлькостi нескiнченно малих складових . Отже

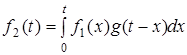. (7.4)

Якщо зробити замiну змiнних 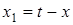, то пiсля перетворень, матимемо

. (7.5)

В теорiї електричних кiл iнтеграли (7.4)-(7.5) мають назву iнтегралiв накладання.

Примiтка. Формулу (7.4) можна отримати, розмiрковуючи трохи iнакше. За визначенням, якщо , тодi за нульових початкових умов 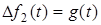; якщо , то . Аби зберегти розмiрнiсть, треба функцiю помножити на площу iмпульсу 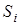, яка для одиничного iмпульсу 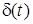дорiвнює одиницi. Для функцiї (рис.7.3г) площа iмпульсу дорiвнює .

Якщо , то за теоремою накладання 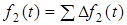. Якщ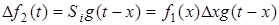о , то . Замiнюючи 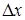на 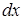i переходячи вiд суми до iнтеграла, отримуємо формулу (7.4).

Переглядів: 999